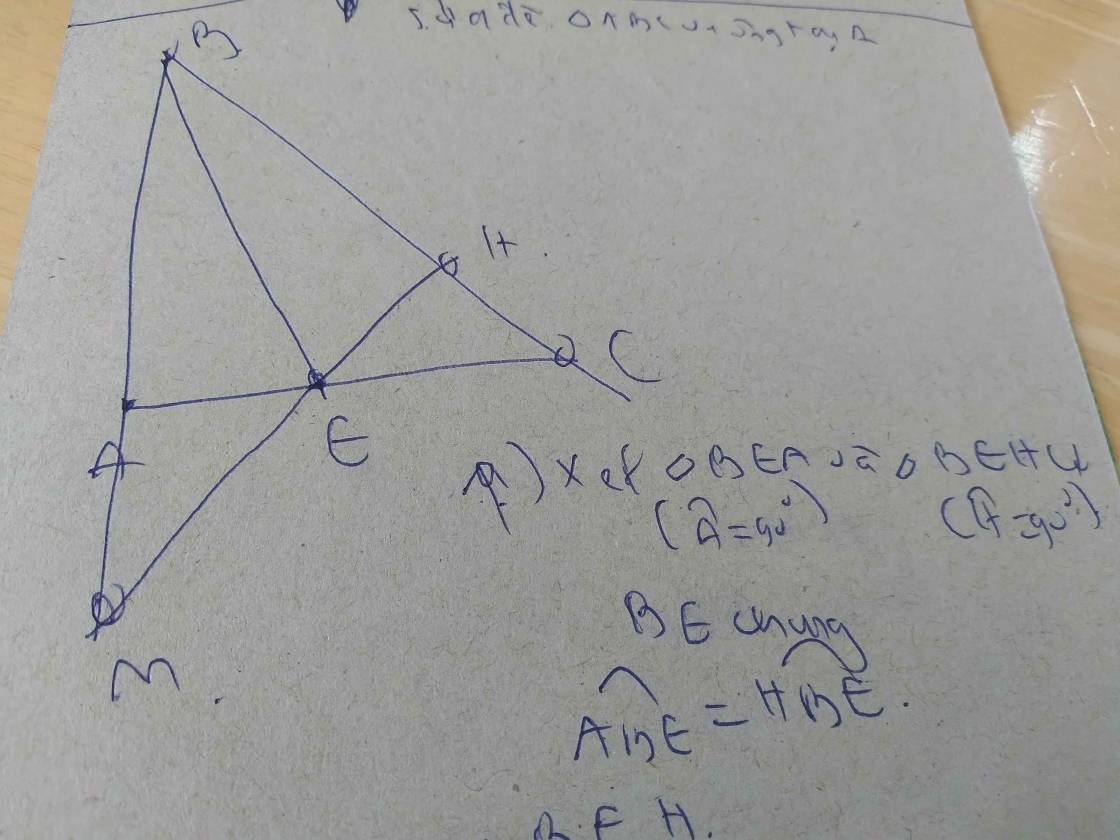
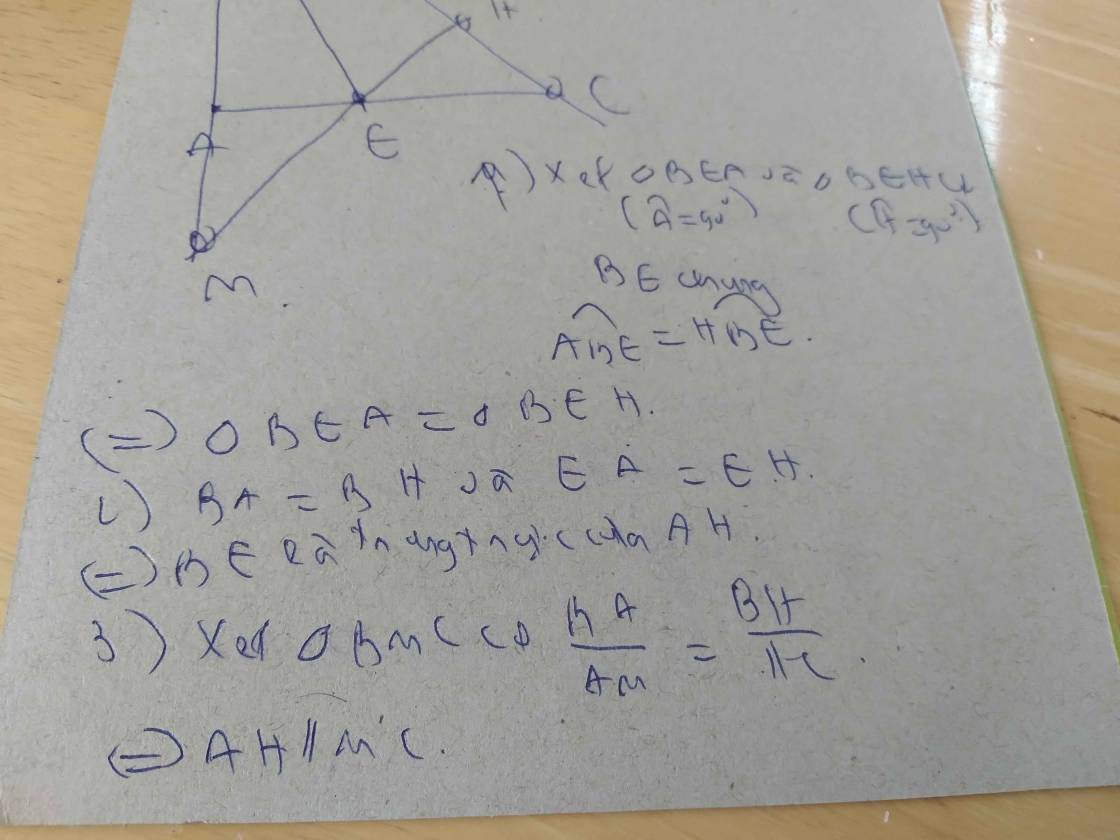
1. Cho \(\Delta\)ABC vuông tại A, đường cao AH. Gọi M,N theo thứ tự là trung điểm của HC và AH. Nối AM với MN. Lấy điểm G trên AM sao cho GM= \(\dfrac{1}{2}\)GA.C/m:
a, \(\Delta\)GAH \(\sim\)\(\Delta\)GMN
b, H,G,N thẳng hàng
2. Cho \(\Delta\)ABC, trung tuyến AD. AB =4cm, AC =8cm. Qua B kẻ đương thẳng ắt A tại F sao cho \(\Lambda\)ABF = \(\Lambda\)ACB. C/m:
a, Tính độ dài CF
b, S\(_{ABC}\) = 2S\(_{ADC}\)
c, Gọi O là giao điểm BF và AD. CO cắt AB tại E. Từ A và C lần lượt kẻ ác đường thẳng // BE cắt OC tại J, cắt AD tại I. C/m: - \(\dfrac{FC}{FA}\)=\(\dfrac{CI}{JA}\)
- \(\dfrac{DB}{DC}\)* \(\dfrac{FC}{FA}\)* \(\dfrac{EA}{EB}\)=1
Chiều mai mình học rồi, các bạn chỉ cần làm bài 1b và bài 2c gạch đầu dòng thứ hai thôi, những ý khác mình làm được rồi.