Trong các hình vẽ sau hình nào là hình thang cân,vì sao:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các hình nội tiếp được trong một đường tròn là:
+ Hình chữ nhật:
Hình chữ nhật ABCD có:
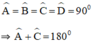
⇒ ABCD nội tiếp trong một đường tròn. Đường tròn đó là đường tròn đường kính AC.
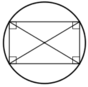
+ Hình vuông:
Vì hình vuông là hình chữ nhật
⇒ Hình vuông cũng nội tiếp trong một đường tròn.
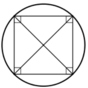
+ Hình thang cân:
Hình thang cân ABCD có:
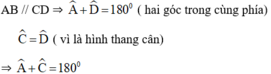
⇒ ABCD nội tiếp trong một đường tròn.

Các hình nội tiếp được trong một đường tròn là:
+ Hình chữ nhật:
Hình chữ nhật ABCD có:
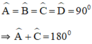
⇒ ABCD nội tiếp trong một đường tròn. Đường tròn đó là đường tròn đường kính AC.
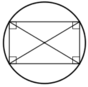
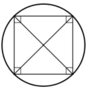
+ Hình vuông:
Vì hình vuông là hình chữ nhật
⇒ Hình vuông cũng nội tiếp trong một đường tròn.
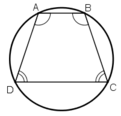
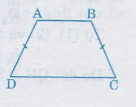
+ Hình thang cân:
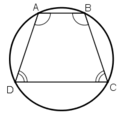
Hình thang cân ABCD có:
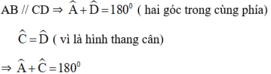
⇒ ABCD nội tiếp trong một đường tròn.

Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng 180o.Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là 90o + 90o = 180o
Hình thang nói chung, hình thang vuông không nội tiếp được đường tròn.
Hình thang cân ABCD (BC= AD) có hai góc ở mỗi đáy bằng nhau
=
,
=
; mà
+
= 180o (hai góc trong cùng phía tạo bởi cát tuyến AD với AD // CD),suy ra
+
= 180o . Vậy hình thang cân luôn có tổng hai góc đối diện bằng 180o nên nội tiếp được đường tròn

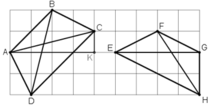
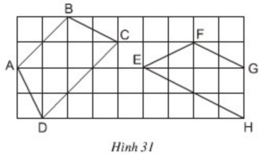
+ Xét tứ giác ABCD
Nhận thấy AB // CD ⇒ Tứ giác ABCD là hình thang.
Xét ΔACK vuông tại K ta có: AC2 = AK2 + KC2 = 42 + 12 = 17
Tương tự ta có BD2 = 42 + 12 = 17
⇒ AC2 = BD2
⇒ AC = BD
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
+ Xét tứ giác EFGH
FG // EH ⇒ Tứ giác EFGH là hình thang.
Lại có : EG = 4cm
FH2 = 22 + 32 = 13 ⇒ FH = √13 ≠ EG.
Vậy hình thang EFGH có hai đường chéo không bằng nhau nên không phải hình thang cân.

Lời giải:
a. $BAC$ là tam giác vuông cân tại $A$
$\Rightarrow \widehat{BCA}=45^0$
$ACE$ là tam giác vuông cân tại $E$
$\Rightarrow \widehat{EAC}=45^0$
Do đó: $\widehat{BCA}=\widehat{EAC}$. Mà 2 góc này ở vị trí so le trong nên $AE\parallel BC$. Mà $\widehat{E}=90^0$ nên $AECB$ là hình thang vuông.
-----------------
Tính góc:
Hình thang vuông $AECB$ có $\widehat{E}=90^0$ đương nhiên $\widehat{C}=180^0-\widehat{E}=90^0$
$\widehat{ABC}=45^0$ (do $ABC$ vuông cân tại $A$)
$\widehat{BAE}=\widehhat{BAC}+\widehat{EAC}=90^0+45^0=135^0$
Tính cạnh:
Vì $ABC$ vuông cân tại $A$ nên $AB=AC$
Áp dụng định lý Pitago:
$AB^2+AC^2=BC^2=4$
$AB^2+AB^2=4$
$2AB^2=4\Rightarrow AB=\sqrt{2}$ (cm)
$\Rightarrow AC=\sqrt{2}$ (cm)
Áp dụng định lý Pitago cho tam giác $ACE$ vuông cân tại $E$:
$AE^2+EC^2=AC^2=2$
$2AE^2=2\Rightarrow AE=1$ (cm)
$EC=AE=1$ (cm)
Vậy.........

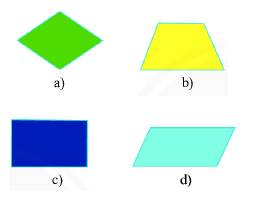
Hình a là hình thoi.
Hình b là hình thang cân.
Hình c là hình chữ nhật.
Hình d là hình bình hành.

Hình thang cân trong các hình thang là : HKIJ (vì có HJ = IK)
hình 1,2,3 là hình thang cân
hình 1: ab//dc ; ab = ac
hình 2: góc h = góc g
hình 3: LI=JR