Cho tam giác ABC cân tại A . Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy điểm N sao cho BM = CN.
a) Chứng minh: △ABM = △ ACN
b) Kẻ BH ⊥ AM ; CK ⊥ AN ( H thuộc AM; K thuộc AN ) . Chứng minh : AH = AK
c) Gọi O là giao điểm của HB và KC . Tam giác OBC là tam giác gì ? Vì sao

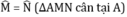

a) Ta có: \(\left\{{}\begin{matrix}\widehat{ABM}+\widehat{ABC}=180^{^O}\\\widehat{ACN}+\widehat{ACB}=180^{^O}\end{matrix}\right.\left(Kềbù\right)\)
Lại có : \(\widehat{ABC}=\widehat{ACB}\text{ (ΔABC cân tại A)}\)
Suy ra : \(180^{^O}-\widehat{ABC}=180^{^O}-\widehat{ACB}\)
\(\Leftrightarrow\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM,\Delta ACN\) có:
\(AB=AC\) (ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\) (cmt)
\(BM=CN\left(gt\right)\)
=> \(\Delta ABM=\Delta ACN\left(c.g.c\right)\)
b) Xét \(\Delta AHB,\Delta AKC\) có:
\(\widehat{AHB}=\widehat{AKC}\left(=90^{^O}\right)\)
\(AB=AC\) (ΔABC cân tại A)
\(\widehat{BAH}=\widehat{CAK}\) [do \(\Delta ABM=\Delta ACN\left(cmt\right)\)]
=> \(\Delta AHB=\Delta AKC\) (cạnh huyền - góc nhọn)
=> AH = AK (2 cạnh tương ứng)
c) Xét \(\Delta HMB,\Delta KNC\) có:
\(\widehat{MHB}=\widehat{NKC}\left(=90^{^O}\right)\)
BM = CN (gt)
\(\widehat{HMB}=\widehat{KNC}\) [do \(\Delta ABM=\Delta ACN\left(cmt\right)\)]
=> \(\Delta HMB=\Delta KNC\) (cạnh huyền -góc nhọn)
=> \(\widehat{HBM}=\widehat{KCN}\) (2 góc tương ứng) (1)
Ta có : \(\left\{{}\begin{matrix}\widehat{HBM}=\widehat{OBC}\\\widehat{KCN}=\widehat{OCB}\end{matrix}\right.\) (đối đỉnh) (2)
Từ (1) và (2) => \(\widehat{OBC}=\widehat{OCB}\)
Do đó: ΔOBC cân tại O (đpcm).