Bài 22 ạ pl
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(\Delta=\left(m+3\right)^2-8m=\left(m-1\right)^2+8>0\) ; \(\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi m
b. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+3}{2}\\x_1x_2=\dfrac{m}{2}\end{matrix}\right.\)
Từ điều kiện: \(x_1=4x_2\) thế vào \(x_1+x_2=\dfrac{m+3}{2}\) ta được:
\(4x_2+x_2=\dfrac{m+3}{2}\Rightarrow x_2=\dfrac{m+3}{10}\Rightarrow x_1=4x_2=\dfrac{2\left(m+3\right)}{5}\)
Thế \(x_1;x_2\) vào \(x_1x_2=\dfrac{m}{2}\) ta được:
\(\left(\dfrac{m+3}{10}\right)\left(\dfrac{2\left(m+3\right)}{5}\right)=\dfrac{m}{2}\)
\(\Leftrightarrow2\left(m+3\right)^2=25m\)
\(\Leftrightarrow2m^2-13m+18=0\Rightarrow\left[{}\begin{matrix}m=2\\m=\dfrac{9}{2}\end{matrix}\right.\)




\(\left(3a-1\right)^2-2\left(3a-1\right)\left(2+b\right)+\left(2+b\right)^2\)
\(=\left(3a-1-b-2\right)^2\)
\(=\left(3a-b-3\right)^2\)

2:
A=(x1+x2)^2-2x1x2-(x1*x2)^2
=(1/2)^2-2*(-3/2)-(-3/2)^2
=1/4-9/4+3
=3-2=1

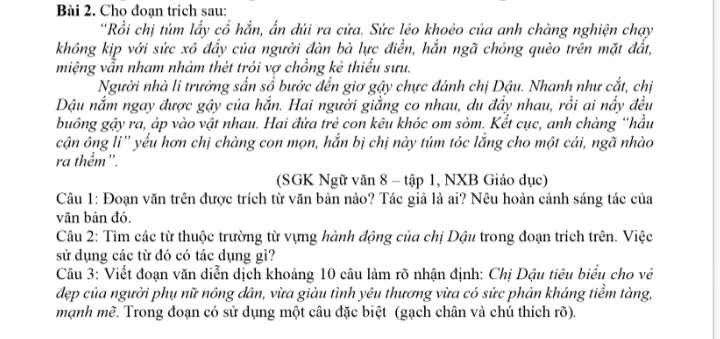


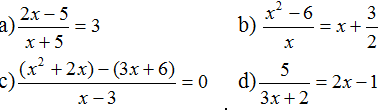
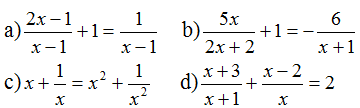
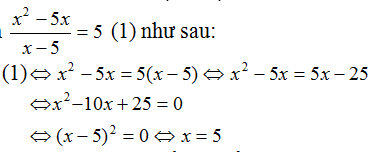

Đặt x là số Z của nguyên tử nguyên tố đó (x:nguyên, dương)
Từ các dữ liệu đề cho, ta có pt:
\(\dfrac{\left(14+x\right).92,2\%+\left(15+x\right).4,7\%+\left(16+x\right).3,1\%}{100\%}=28,109\\ \Leftrightarrow x=14\)
=> Số khối các đồng vị của nguyên tố đó:
A1=14+14=28(đ.v.C)
A2=15+14=29(đ.v.C)
A3=16+14=30(đ.v.C)