Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó; ABCD là hình bình hành
Suy ra: AB//CD
c: Xét ΔOMI vuông tại I và ΔONF vuông tại F có
OM=ON
\(\widehat{MOI}=\widehat{NOF}\)
Do đó: ΔOMI=ΔONF
Suy ra: MI=NF
a: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
b: Xét ΔAOM và ΔCON có
\(\widehat{AOM}=\widehat{CON}\)
OA=OC
\(\widehat{OAM}=\widehat{OCN}\)
Do đó: ΔAOM=ΔCON
Suy ra: OM=ON
hay O là trung điểm của MN
Xét tứ giác AMCN có
O là trung điểm của AC
O là trung điểm của MN
Do đó: AMCN là hình bình hành
Suy ra: AM//CN
a) xét \(\Delta DOC,\Delta BOA:\)
\(\widehat{DOC}=\widehat{BOA}\left(đđ\right)\)
OA = OC ( gt )
OD = OB ( gt )
\(\rightarrow\Delta DOC=\Delta BOA\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODC}=\widehat{OBA}\) ( 2 góc tương ứng )
mà chúng lại nằm ở vị trí so le trong
\(\Rightarrow\) AB// CD
c) xét \(\Delta IOM,\Delta FON:\)
ON = OM ( \(\Delta AOM=\Delta CON\) )
\(\widehat{O_1}=\widehat{O_2}\) ( đđ)
\(\widehat{I}=\widehat{F}=90^o\left(gt\right)\)
\(\rightarrow\Delta IOM=\Delta FON\) ( cạnh huyền góc nhọn )
\(\Rightarrow MI=NF\) ( 2 cạnh tương ứng )
1.a. xet tam giac ABD va tam giac CDE co : b.B1=B2=450ma vi cai cau a nen C1=C2=450. Vay C=900
AD=AC (vi D la trung diem cua AC) 2.a Xet tam giac ODC va tam giac OAB co
DB = DE (gt) OA=OC(gt) ; OD= OB (gt) ; goc DOC=goc AOB
goc ADB = goc EDC (doi dinh) Suy ra tam giac ODC=tam giac OAB (c.g.c) . Vay AB song
suy ra tam giac ABD = tam giac CDE (c.g.c) song voi CD . HET GIAY RUI
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
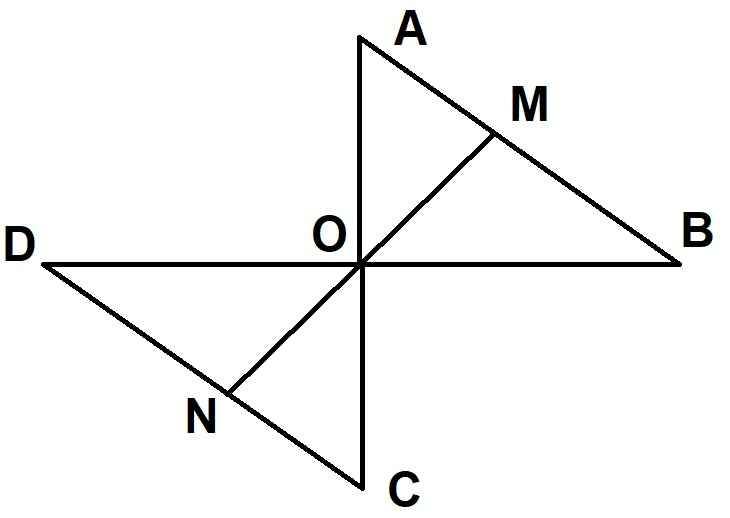
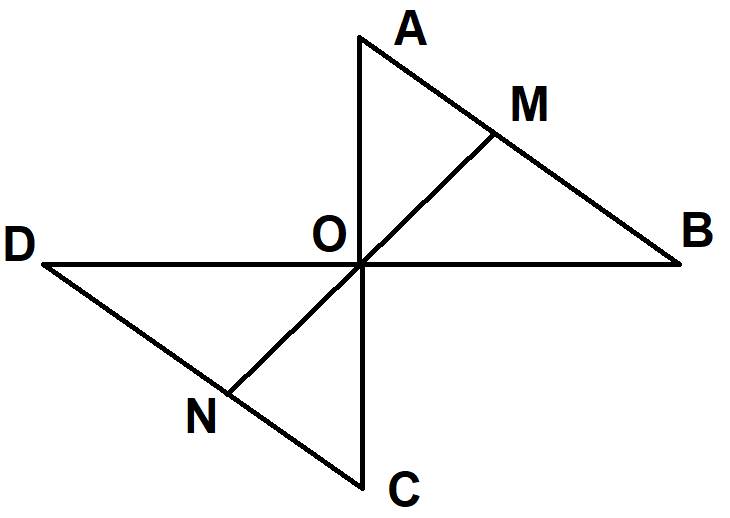
có đẹp không ạ 
a) Xét \(\Delta AOB\) và \(\Delta ADC\) có :
\(DA=AB\left(gt\right)\)
\(\widehat{DAC}=\widehat{BAO}\) (đối đỉnh)
\(CA=AO\left(gt\right)\)
=> \(\Delta AOB\) = \(\Delta ADC\) (c.g.c)
=> \(\widehat{CDA}=\widehat{ABO}\) (2 góc tương ứng)
Mà : 2 góc này ở vị trí so le trong
=> \(\text{AB//CD}\left(đpcm\right)\)
a) Xét ΔΔCDO và ΔΔABO có:
DO = BO (giả thiết)
DOCˆDOC^ = BOAˆBOA^ (đối đỉnh)
CO = AO (giả thiết)
=> ΔΔCDO = ΔΔABO (c.g.c)
=> CD = AB (2 cạnh tương ứng)
b) Vì ΔΔCDO = ΔΔABO (câu a)
nên DCOˆDCO^ = BAOˆBAO^ (2 góc tương ứng)
hay NCOˆNCO^ = MAOˆMAO^ và MBOˆMBO^ = NDOˆNDO^ (2 góc tương ứng)
Xét ΔΔMAO và ΔΔNCO có:
MAOˆMAO^ = NCOˆNCO^ (chứng minh trên)
AO = CO (giả thiết)
AOMˆAOM^ = COMˆCOM^ (đối đỉnh)
=> ΔΔMAO = ΔΔNCO (g.c.g)
=> MA = NC (2 cạnh tương ứng) →→ đpcm
Xét ΔΔMBO và ΔΔNDO có:
MBOˆMBO^ = NDOˆNDO^ (chứng minh trên)
BO = DO (giả thiết)
MOBˆMOB^ = NODˆNOD^ (đối đỉnh)
=> ΔΔMBO = ΔΔNDO (g.c.g)
=> MB = ND (2 cạnh tương ứng)
c) Ta có:
AM + MB = AB
CN + ND = CD
mà MB = ND (câu b); AB = CD (câu a)
nên AM = CN
Do ΔΔMAO = ΔΔNCO (câu b)
nên MAIˆMAI^ = NCFˆNCF^ (2 góc tương ứng)
Xét ΔΔAIM vuông tại I và ΔΔCFN vuông tại F có:
AM = NC (chứng minh trên)
MAIˆMAI^ = NCFˆNCF^ (chứng minh trên)
=> ΔΔAIM = ΔΔCFN (cạnh huyền - góc nhọn)
=> MI = FN (2 cạnh tương ứng)