Bằng đồ thị hàm hãy biện luận số nghiệm của phương trình \(\left|x\right|+\left|x+1\right|=m\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
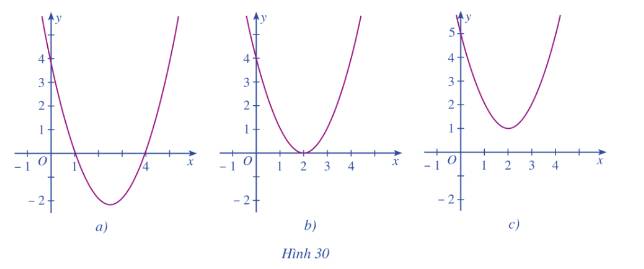
Hình 30a:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \left( {1;4} \right)\)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right] \cup \left[ {4; + \infty } \right)\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left[ {1;4} \right]\)
Hình 30b:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left\{ 2 \right\}\)
Hình 30c:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \emptyset \)
27 tháng 4 2022
có:
+) đạo hàm của f(x) = f'(x) = 3x2
+) phương trình tiếp tuyến là : y= f'(x).(x-x0) + f(x0)
=> y = 3x2.(x-1) + 13 + 3 = 3x3 - 3x2 + 4