Một họ 12 đường thẳng song song cắt một họ khác gồm 9 đường thẳng song song ( không song song với 12 đường ban đầu) . Có bao nhiêu hình bình hành được tạo lên?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 6 2019
Cách 1:
Nhận xét: cứ 2 đường thẳng họ này kết hợp với 2 đường thẳng họ kia sẽ tạo thành 1 hình bình hành.
Số cách chọn 2 đthẳng mỗi họ:
3x2:2=3cách
5x4:2=10cách
-->Số hình bình hành tạo thành: 3x10=30 hình bình hành
Cách 2:
Trước hết, ta chứng minh giao điểm của 2 đthẳng là đỉnh của 3x5=15 hình bình hành.
Qua mỗi giao điểm có 2 đthẳng là 2 cạnh của hình bình hành, như vậy ta kết hợp 1 cặp đthẳng song song với chúng là ta được 1 hình bình hành.
Số cặp đthẳng song song với chúng:
(3-1)x(5-1)=8cặp
Số giao điểm: 3x5=15
Số hình bình hành có thể tạo thành là:
15x8=120 hình bình hành
Nhưng hình bình hành có 4 đỉnh nên số hình bình hành thực tế được tạo thành chỉ có:
120:4=30 hình bình hành
CM
28 tháng 10 2019
Cách 1: Nhận xét: cứ 2 đường thẳng họ này kết hợp với 2 đường thẳng họ kia sẽ tạo thành 1 hình bình hành. Số cách chọn 2 đthẳng mỗi họ: 3x2:2=3cách 5x4:2=10cách -->Số hình bình hành tạo thành: 3x10=30 hình bình hành Cách 2: Trước hết, ta chứng minh giao điểm của 2 đthẳng là đỉnh của 3x5=15 hình bình hành. Qua mỗi giao điểm có 2 đthẳng là 2 cạnh của hình bình hành, như vậy ta kết hợp 1 cặp đthẳng song song với chúng là ta được 1 hình bình hành. Số cặp đthẳng song song với chúng: (3-1)x(5-1)=8cặp Số giao điểm: 3x5=15 Số hình bình hành có thể tạo thành là: 15x8=120 hình bình hành Nhưng hình bình hành có 4 đỉnh nên số hình bình hành thực tế được tạo thành chỉ có: 120:4=30 hình bình hành
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
Ta thấy rằng, cứ 2 đường thẳng song song cắt 2 đường thẳng song song khác thì tạo thành một hình bình hành
Do đó, hình bình hành tạo thành được xác định qua 2 công đoạn
Công đoạn 1: Chọn 2 đường thẳng trong 4 đường nằm ngang, có:
\(C_4^2 = \frac{{4!}}{{2!.2!}} = 6\)
Công đoạn 2: Chọn 2 đường thẳng trong 5 đường xiên, có: \(C_4^2 = \frac{{5!}}{{2!.3!}} = 10\)
Vậy số hình bình hành được tạo thành là: \(6.10 = 60\) (hình bình hành)
25 tháng 3 2023
Số hình bình hành tạo thành là: \(C^2_{10}\cdot C^2_9=1620\left(đường\right)\)
CM
2 tháng 5 2019
Cứ hai đường thẳng song song trong nhóm A và hai đường thẳng song song trong nhóm B tạo thành một hình bình hành.
Chọn 2 đường trong 10 đường của nhóm A có 
cách.
Chọn 2 đường trong 8 đường của nhóm B có 
cách.
Vậy số hình bình hành tạo thành là 
hình.
Chọn D.
CM
11 tháng 8 2019
Đáp án C
Gọi 
là 4 đường thẳng song song với BC.
Gọi 
là 5 đường thẳng song song với AC.
Gọi 
là 6 đường thẳng song song với AB.
Cứ 2 đường thẳng song song và hai đường thẳng không song song tạo thành một hình thang.
Vậy số hình thành là
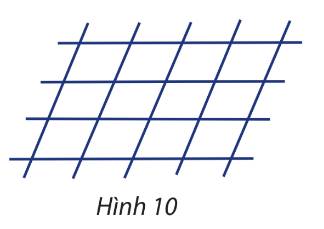
1 hình bình hành được tạo bởi 2 cặp đt song song
Số hình bình hành đc tạo ra là 12C2.9C2=2376 hình
một hình bình hành sẽ được tạo nên từ 2 đường thẳng // trong số 12 đường thẳng và 2 đường thẳng // trong số 9 đường thẳng
- chọn 2 trong số 12 đường thẳng // có C212 cách
- chọn 2 trong số 9 đường thẳng // có C29 cách
vậy số hình bình hành dựng được là C212.C29 = 2376 hình