Cho hcn ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy F sao cho AE= CF ( E khác A,B; f khác C và D)
a, cm AECF là hbh
P là tđ À, Q là tđ Ce, tg DPQC là hình j
gọi O là tđx ABCD, I, K ,G là hình chiếu B, D, O trên AF , cm Glag tđ IK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 11 2021
Vì AE=CF và AE//CF (AB//CD do hbh ABCD) nên AECF là hbh
\(\left\{{}\begin{matrix}AE=CF\\AM=CN\\\widehat{A}=\widehat{C}\left(hbh.ABCD\right)\end{matrix}\right.\Rightarrow\Delta AME=\Delta CNF\left(c.g.c\right)\\ \Rightarrow ME=NF\left(4\right)\\ \left\{{}\begin{matrix}AE=CF\\AB=CD\end{matrix}\right.\Rightarrow AB-AE=CD-CF\Rightarrow BE=DF\left(1\right)\\ \left\{{}\begin{matrix}AM=CN\\AD=BC\end{matrix}\right.\Rightarrow AD-AM=CN-BC\Rightarrow DM=BN\left(2\right)\)
ABCD là hbh nên \(\widehat{B}=\widehat{D}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\Delta DMN=\Delta BFE\left(c.g.c\right)\\ \Rightarrow MN=EF\left(5\right)\)
(4)(5) suy ra MENF là hbh
24 tháng 2 2020
a) Xét tam giác ADB có:
\(\frac{AE}{AB}=\frac{AH}{AD}\left(gt\right)\)
\(\Rightarrow HE//DB\left(1\right)\)( định lý Ta-let đảo )
Xét tam giác CDB có:
\(\frac{CF}{CB}=\frac{CG}{CD}\left(gt\right)\)
\(\Rightarrow GF//BD\left(2\right)\)
Từ (1) và (2) \(\Rightarrow HE//GF\)
CMTT\(HG//EF\)( cùng // AC)
Xét tứ giác EFGH có:
\(\hept{\begin{cases}HE//GF\left(cmt\right)\\HG//EF\left(cmt\right)\end{cases}\Rightarrow EFGH}\)là hình bình hành (dhnb)
b)
Đặt\(\frac{AE}{AB}=\frac{AH}{AD}=\frac{CF}{CB}=\frac{CG}{CD}=k\)
Xét tam giác ADB có:
\(HE//BD\left(gt\right)\)
\(\Rightarrow\frac{HE}{BD}=\frac{AE}{AB}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{HE}{BD}=k\)( vì \(\frac{AE}{AB}=k\))
\(\Rightarrow HE=k.BD\)
Xét tam giác ABC có:
\(EF//AC\left(cmt\right)\)
\(\Rightarrow\frac{EF}{AC}=\frac{BE}{BA}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{EF}{AC}=\frac{AB-AE}{BA}=1-k\)
\(\Rightarrow EF=\left(1-k\right)AC\)
\(P_{EFGH}=2\left(HE+EF\right)\)
\(=2\left[k.BD+\left(1-k\right)AC\right]\)
\(=2AC\)không đổi ( AC=BD do ABCD là hình chữ nhật )
Vậy chu vi của hbh EFGH có giá trị không đổi
CM
29 tháng 1 2018
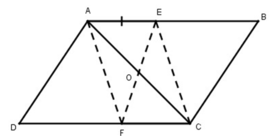
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét tứ giác AECF:
AB // CD (gt)
⇒ AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
⇒ AC và EF cắt nhau tại trung điểm mỗi đường
OA = OC ( tính chất hình bình hành) ⇒ EF đi qua O
Vậy AC, BD, EF đồng quy tại O.
19 tháng 10 2021
a, Vì \(AE=CF\) và AE//CF (AB//CD) nên AECF là hbh
b, Ý bạn là O là giao điểm của AC và BD đúng k?
Vì ABCD là hbh mà O là giao điểm AC và BD nên O là trung điểm AC,BD
Ta có AECF là hbh
Mà O là trung điểm AC nên là trung điểm EF
Do đó O;E;F thẳng hàng
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Ta có: ΔADF vuông tại D
mà DP là đường trung tuyến
nên PD=PF
=>\(\widehat{AFD}=\widehat{PDF}\)
=>\(\widehat{PDF}=\widehat{QCD}\)
Xét tứ giác PQCD có PQ//CD
nên PQCD là hình thang
mà \(\widehat{PDC}=\widehat{QCD}\)
nên PQCD là hình thang cân