Tìm hệ số lớn nhất trong khai triển (1+2x/3)10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2018
ta có : \(\left(1+\dfrac{2x}{3}\right)^{10}=\sum\limits^{10}_{k=0}\left(\dfrac{2}{3}\right)^k.x^k\)
vì \(0< \dfrac{2}{3}< 1\) \(\Rightarrow\left(\dfrac{2}{3}\right)^{k-1}>\left(\dfrac{2}{3}\right)^k\)
mà vì \(K\in N\)
\(\Rightarrow\) hệ số lớn nhất trong khai triển \(\left(1+\dfrac{2x}{3}\right)^{10}\) là \(\left(\dfrac{2}{3}\right)^0=1\)
AH
Akai Haruma
Giáo viên
13 tháng 12 2017
Lời giải:
Theo khai triển nhị thức Newton ta có:
\(\left ( 1+\frac{2x}{3} \right )^{10}=\sum _{k=0}^{10}C^{k}_{10} 1^{k}\left ( \frac{2x}{3} \right )^{10-k}\)
\(=C^{0}_{10}\left ( \frac{2x}{3} \right )^{10}+C_{10}^{1}\left ( \frac{2x}{3} \right )^9+.....+C_{10}^{10}\left ( \frac{2x}{3} \right )^0\)
Các hệ số: \(C_{10}^0(\frac{2}{3})^{10}; C_{10}^{1}(\frac{2}{3})^9; ...; C_{10}^{10}(\frac{2}{3})^0\)
Xét hàm: \(f(x)=C_{10}^{x}\left(\frac{2}{3}\right)^{10-x}\)
\(f(a+1)=C_{10}^{a+1}(\frac{2}{3})^{9-a}\)
\(f(a)=C_{10}^{a}\left(\frac{2}{3}\right)^{10-a}\)
\(f(a+1)-f(a)=\frac{10!}{(a+1)!(9-a)!}\frac{2^{9-a}}{3^{9-a}}-\frac{10!}{a!(10-a)!}\frac{2^{10-a}}{3^{10-a}}\)
\(=\frac{10!.2^{9-a}}{a!(9-a)!.3^{9-a}}\left[ \frac{1}{a+1}-\frac{2}{3(10-a)}\right]\)
\(=\frac{10!.2^{9-a}}{a!(9-a)!.3^{9-a}}.\frac{28-5a}{3(a+1)(10-a)}\)
Nếu \(a\geq 6\Rightarrow f(a+1)-f(a)< 0\Rightarrow \) hàm giảm
Nếu \(a\leq 6\Rightarrow f(a+1)-f(a)> 0\) , hàm tăng
Do đó điểm cực đại của \(f(x)\) với \(x=0;1;2;....; 10\) đặt tại \(x=6\)
Do đó hệ số lớn nhất là: \(C_{10}^{6}(\frac{2}{3})^4=\frac{1120}{27}\)
30 tháng 12 2018
bạn ơi cho mình hỏi !
tại sao giá trị k ở C lại là 6 mà (2/3)4
T
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
SHTQ: \(C_{10}^k.2^k.x^{10-k}\) có hệ số: \(a_k=C_{10}^k2^k\)
Hệ số lớn nhất khi thỏa mãn:
\(\left\{{}\begin{matrix}a_k\ge a_{k+1}\\a_k\ge a_{k-1}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}C_{10}^k2^k\ge C_{10}^{k+1}2^{k+1}\\C_{10}^k2^k\ge C_{10}^{k-1}2^{k-1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10!}{k!\left(10-k\right)!}\ge\dfrac{10!}{\left(k+1\right)!\left(10-\left(k+1\right)\right)!}.2\\\dfrac{10!}{k!\left(10-k\right)!}.2\ge\dfrac{10!}{\left(k-1\right)!\left(10-\left(k-1\right)\right)!}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{10-k}\ge\dfrac{2}{k+1}\\\dfrac{2}{k}\ge\dfrac{1}{11-k}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}k\ge\dfrac{19}{3}\\k\le\dfrac{22}{3}\end{matrix}\right.\) \(\Rightarrow k=7\)
Hệ số lớn nhất: \(C_{10}^7.2^7\)
HT
3 tháng 2 2021
\(\left(2x^3-\dfrac{3}{x^2}\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.2^k.3^{10-k}.x^{3k}.\dfrac{1}{x^{2\left(10-k\right)}}\)
\(x^{10}=\dfrac{x^{3k}}{x^{20-2k}}\Leftrightarrow3k-20+2k=10\Leftrightarrow5k=30\Leftrightarrow k=6\)
\(\Rightarrow he-so:2^k.3^{10-k}=2^6.3^4=..\)
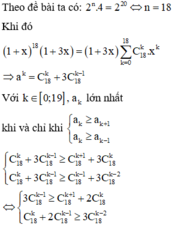
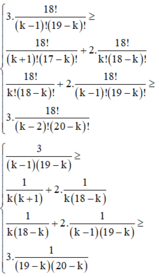
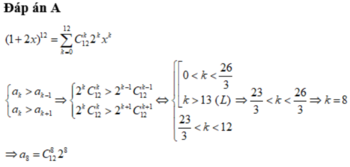
mk bổ sung thêm hằng đẳng thức cho các bạn nha .
ta có : \(\left(a+b\right)^{10}=a^{10}+10a^9b+45a^8b^2+120a^7b^3+210a^6b^4+252a^5b^5+210a^4b^6+120a^3b^7+45a^2b^8+10ab^9+b^{10}\)
\(\Rightarrow\left(1+\dfrac{2x}{3}\right)^{10}=1+\dfrac{20x}{3}+20x^2+\dfrac{320x^3}{9}+\dfrac{1120x^4}{27}+\dfrac{896x^5}{27}+\dfrac{4480x^6}{243}+\dfrac{5120x^7}{729}+\dfrac{1280x^8}{729}+\dfrac{5120x^9}{19683}+\dfrac{340x^{10}}{19683}\)
ta thấy hệ số lớn nhất trong khai triển này là \(\dfrac{1120}{27}\)
vậy hệ số lớn nhất trong khai triển \(\left(1+\dfrac{2x}{3}\right)^{10}\) là \(\dfrac{1120}{27}\) .
nhớ hok thuộc hằng đẳng thức mới này nha
.