Tìm k để 3 điểm sau thẳng hàng M ( 2; -1), N (1; 1 ) và P ( 3; k + 1).
Em cần gấp lắm ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tìm k để 3 điểm sau thẳng hàng M ( 2; -1), N (1; 1 ) và P ( 3; k + 1).
Gọi phương trình đường thẳng đi qua 2 điểm M, N là y = ax + b
Khi đó ta có:
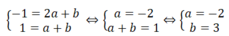
Phương trình đường thẳng MN là: y = - 2x + 3
Để 3 điểm M, N, P thẳng hàng thì P nằm trên đường thẳng MN
⇔ k + 1 = -2.3 + 3 ⇔ k + 1 = -3 ⇔ k = -4 (Thỏa mãn ĐK)


a: vì M nằm trên trục Ox nên M(x;0)
\(\overrightarrow{MA}=\left(x_A-x_M;y_A-y_M\right)=\left(-3-x_M;2\right)\)
\(\overrightarrow{MB}=\left(x_B-x_M;y_B-y_M\right)=\left(4-x_M;3\right)\)
Ta có: ΔMAB vuông tại M
nên \(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\)
\(\Leftrightarrow\left(-3-x_M\right)\left(4-x_M\right)+6=0\)
\(\Leftrightarrow\left(x_M+3\right)\left(x_M-4\right)+6=0\)
\(\Leftrightarrow x_M^2-x_M-6=0\)
=>xM=3

theo mk nghĩ thôi nha
bh bn có thể vẽ tọa độ của hai điểm A và B sau đó kẻ đoạn AB,
do điểm C có x= 3 mà nếu như y > 0 thì A,B,C sẽ không thẳng hàng ,vậy bắt buộc y phải < 0 từ đó dóng từ số 3 thẳng xuống sẽ cắt đoạn AB và giao điểm đó sẽ là điểm C, sau đó ta vạch đều trục tung y ở phía dưới rồi dóng điểm cắt đấy với số tương ứng
sau đó lấy số đó trừ cho một sẽ ra số cần tìm
mk ko bt vẽ đồ thị trên này nên chỉ ghi lí thuyết thôi nha
mk vẽ ra vở là m nó sẽ bằng -4 vì khi dóng ta được -3 nhưng muốn tìm m ta trừ đi sẽ ra -4
có j ko hiểu thì cứ hỏi mk nha ![]()

Ta có:
\(\vec{AN}=\vec{AM}+\vec{MN}\)
\(=\dfrac{2}{3}\vec{AC}+\dfrac{1}{4}\vec{MB}\)
\(=\dfrac{2}{3}\vec{AC}+\dfrac{1}{4}\left(\vec{AB}-\vec{AM}\right)\)
\(=\dfrac{1}{4}\vec{AB}+\dfrac{1}{2}\vec{AC}\)
\(\vec{AP}=\vec{AC}+\vec{CP}\)
\(=\vec{AC}+\dfrac{1}{k+1}\vec{CB}\)
\(=\vec{AC}+\dfrac{1}{k+1}\left(\vec{AB}-\vec{AC}\right)\)
\(=\dfrac{1}{k+1}\vec{AB}+\dfrac{k}{k+1}\vec{AC}\)
A, N, P thẳng hàng khi:
\(\dfrac{\dfrac{k}{k+1}}{\dfrac{1}{k+1}}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{4}}\Leftrightarrow k=2\)
Kết luận: \(k=2\)