1. Cho hình bình hành ABCD có diện tích là 30m2. Gọi M,N,I,K theo thứ tự là trung điểm của AB, BC, CD, DA. Gọi E, F theo thứ tự là giao điểm của KB với AI và MC. Gọi H và G theo thứ tự là giao điểm củ...

HP

Hồ Phước

3 tháng 12 2017

Câu hỏi hay

1. Cho hình bình hành ABCD có diện tích là 30m2. Gọi M,N,I,K theo thứ tự là trung điểm của AB, BC, CD, DA. Gọi E, F theo thứ tự là giao điểm của KB với AI và MC. Gọi H và G theo thứ tự là giao điểm của DN với AI và MC. a. CM: S_EFGH=2/5 S_AMCI b. Tính S_EFGH? 2. Cho hình thang vuông ABCD (góc A=D=90 độ). Đường cao BH, AC cắt BH tại E. CD=2AB. CM:...

Đọc tiếp

#Toán lớp 8

0

HV

Hồ Văn

15 tháng 8 2017 - olm

Cho hình bình hành ABCD có diện tích S. Gọi M, N, I, K theo thứ tự là trung điểm của AB, BC, CD, DA. Gọi E, F theo thứ tự là giao điểm của KB với AI và MC. Gọi H và G theo thứ tự là giao điểm của DN với AI và MC.

a. CM: S_EFGH=2/5 S_AMCI

b. Tính S_EFGH theo S

#Toán lớp 8

2

HT

Hoàng Thị Thu Hiền

15 tháng 8 2017

xin lỗi nhé mình ko biết

Đúng(0)

TA

Trần Anh

16 tháng 8 2017

a) - Xét tứ giác AMCI , có :

+ AM // CI ( GT )

+ AM = CI ( GT )

=> AMCI là hình bình hành ( 2 cạnh đối song song và bằng nhau )

=> AI // MC hay EH // FG (1)

- XÉt tứ giác BNDK có :

+ BN // DK ( GT )

+ BN = DK ( GT : N , K lần lượt là trung điểm BC , DA và BC = DA )

=> BNDK là hình bình hành ( 2 cạnh đối song song và bằng nhau )

=> BK // DN hay EF // HG ( 2)

- Từ 1 và 2 ta có : EFGH là hình bình hành ( các cặp cạnh đối song song )

- Kẻ FQ vuông góc AI tai Q

=> \(S_{EFGH\:}=FQ.EH\)

- Mặt khác : \(S_{AMCI}=FQ.AI\)( Vì MC // AI nên FQ là đường cao chung )

=> \(\frac{S_{EFGH\:}}{S_{AMCI}}=\frac{FQ.EH}{FQ.AI}=\frac{EH}{AI}\)(3)

- LẠi có :

+ Xét tam giác AHD có : KE // DH và K là trung điểm của AD nên => E là trung điểm của AH hay AE = EH

+ Xét tam giác DCG có : HI // CG , I là trung điểm của DC nên => H là trung diểm của DG => HI là đường trung bình của tam giác DCG => \(HI=\frac{1}{2}.CG\)mà CG = FG = EH nên \(HI=\frac{1}{2}.EH\)

=> \(AI=AE+EH+HI=2.EH+\frac{1}{2}.EH=\frac{5.EH}{2}\)

Thay vào 3 , ta được :

\(\frac{S_{EFGH\:}}{S_{AMCI}}=\frac{EH}{AI}=EH:\frac{5.EH}{2}=\frac{2.EH}{5.EH}=\frac{2}{5}\)

b) - Kẻ AP vuông góc với CD tại Q

- Ta có : \(S_{ABCD}=AP.CD\)và \(S_{AMCI}=AP.CI\)

=> \(\frac{S_{AMCI}}{S_{ABCD}}=\frac{AP.CI}{AP.CD}=\frac{CI}{CD}=\frac{1}{2}\Rightarrow S_{AMCI}=\frac{1}{2}.S_{ABCD}\)

Từ ý a , ta có : \(S_{EFGH\:}=\frac{2}{5}.SAMCI=\frac{2}{5}.\frac{1}{2}.S_{ABCD}=\frac{1}{5}.S_{ABCD}\)

MÀ ABCD có diện tích là S nên \(S_{EFGH\:}=\frac{1}{5}.S\)

Đúng(0)

PT

Pham Trong Bach

22 tháng 12 2019

Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành.

#Toán lớp 8

1

CM

Cao Minh Tâm

22 tháng 12 2019

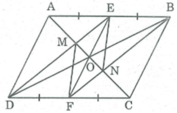
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)

OE = OF (tính chất hình bình hành)

∠ (MOE)= ∠ (NOF) (đối đỉnh )

Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON

Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).

Đúng(1)

HT

Hoa Thiên Cốt

10 tháng 10 2018 - olm

Bài 1: Cho điểm O nằm trong tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Gọi M, N, P, Q theo thứ tự là các điểm đối xứng với O qua E, qua F, qua G, qua H. CMR: MNPQ là hình bình hành và có các cạnh bằng các đường chéo của tứ giác ABCD.

#Toán lớp 8

0

M

Mochi

25 tháng 7 2017 - olm

Cho hình bình hành ABCD. Gọi E,F theo thứ tự là trung điểm của AB, CD. Gọi M,N theo thứ tự là giao điểm của BD với AF, CE.CM: DM=MN=NB

#Toán lớp 8

1

NC

Nhok Cô Đơn

19 tháng 9 2017

mk cũng đang cần lời giải

Đúng(0)

KL

Kiên Lê Duy

21 tháng 10 2021

Cho hình vuông ABCD. Gọi E, F, I theo thứ tự là trung điểm BC, CD, DA. Gọi H, K theo thứ tự là giao điểm của IB, DE với AF. Chứng minh rằng:

a) AH = HK

b) IB vuông góc với AF

#Toán lớp 8

0

LV

Lưu Vân Anh

16 tháng 1 2022 - olm

cho hình bình hành abcd.gọi m,n,i,k theo thứ tự là trung điểm của ab,bc,cd,da.gọi giao điểm của AI với kb,dn theo thứ tự là e,h. họi giao điểm của cm với kb ,dn theo thứ tự là f,g.chứng minh rằng : a, ae=eh=gc. b, Segh=1/5Sabcd

#Toán lớp 8

0

PT

Pham Trong Bach

25 tháng 11 2019

Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: EMNF là hình bình hành

#Toán lớp 8

1

CM

Cao Minh Tâm

25 tháng 11 2019

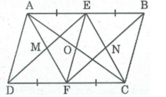
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

+) Ta có:

AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).

Và AB = CD (tính chất hình bình hành)

Suy ra: AE = CF

+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF

Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành

⇒ AF //CE hay EN // FM (1)

Xét tứ giác BFDE ta có:

AB // CD (gt) hay BE // DF

BE = 1/2 AB (gt)

DF = 1/2 CD (gt)

AB = CD (tính chất hình bình hành)

Suy ra: BE = DF

Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)

Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)

Đúng(0)

NH

nguyen hong nhung

13 tháng 12 2021 - olm

Cho hình bình hành ABCD, ab=2ad. gọi E,F theo thứ tự là trung điểm của AB và CD a) c/m tứ giác AECF là hình bình hành b) c/m AF vuông góc DE c) Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.c/m EF=MN d) Tính tỷ số diện tích của tam giác BEF và diện tích hình bình hành ABCD

#Toán lớp 8

0

NM

Namikaze Minato

17 tháng 8 2016 - olm

Cho hình thang ABCD ( AB // CD) có diện tích là S, Cd = 3/2AB. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tính diện tích tứ giác EMFN theo S

#Toán lớp 9

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP