Cho đường tròn (O) bán kính R và dây AB =1,6R. Vẽ 1 tiếp tuyến song song với AB cắt tia AB tại MN. Tính SOMN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
SB
Sonyeondan Bangtan
6 tháng 3 2020
Đúng(0)
Những câu hỏi liên quan
CM
22 tháng 3 2019
a, HS tự chứng minh
b, Ta chứng minh được tứ giác BCEN là hình bình hành => BC = EN
Do BCDE là hình bình hành
=> BC = ED; DE = EN
=> BA ⊥ EN => BABC
=> BC là tiếp tuyến
6 tháng 12 2023
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó:ΔACB vuông tại C
=>\(\widehat{ACB}=90^0\)
Ta có: ΔOAC cân tại O(OA=OC)
mà OH là đường trung tuyến
nên OH\(\perp\)AC và OH là tia phân giác của góc AOC
Ta có: OH\(\perp\)AC(cmt)
AC\(\perp\)CB tại C(Do ΔACB vuông tại C)
Do đó: OH//BC
b:
OH là phân giác của góc AOC
=>\(\widehat{AOH}=\widehat{COH}\)
mà M\(\in\)OH
nên \(\widehat{AOM}=\widehat{COM}\)
Xét ΔOCM và ΔOAM có
OC=OA
\(\widehat{COM}=\widehat{AOM}\)
OM chung
Do đó: ΔOCM=ΔOAM
=>\(\widehat{OCM}=\widehat{OAM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{OAM}=90^0\)
=>OA\(\perp\)MA tại A
=>MA là tiếp tuyến tại A của (O)
28 tháng 4 2023
Xét (O'): \(O'A\perp AB\) tại A và O'A là bán kính.
\(\Rightarrow\)AB là tiếp tuyến của (O') tại A.
\(\Rightarrow\widehat{NAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AN.
Mặt khác \(\widehat{AMN}\) là góc nội tiếp chắn cung AN.
\(\Rightarrow\widehat{AMN}=\widehat{NAB}\left(1\right)\)
Xét (O): \(\widehat{AMC}=\widehat{ABC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{NAB}=\widehat{ABC}\) nên AN//BC.
2 tháng 12 2023
a: Sửa đề: cắt tiếp tuyến tại A của đường tròn ở C
ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
b:ΔOAC=ΔOBC
=>CB=CA
=>C nằm trên đường trung trực của AB(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
từ (1) và (2) suy ra OC là đường trung trực của BA
=>OC\(\perp\)AB
mà OC//AD
nên AB\(\perp\)AD
=>ΔABD vuông tại A
Ta có: ΔABD vuông tại A
=>ΔABD nội tiếp đường tròn đường kính DB
mà ΔABD nội tiếp (O)
nên O là trung điểm của DB
=>D,O,B thẳng hàng
Xét ΔAKD vuông tại K và ΔCAO vuông tại A có
\(\widehat{ADK}=\widehat{COA}\)(hai góc so le trong, AD//CO)
Do đó: ΔAKD\(\sim\)ΔCAO
CM
7 tháng 9 2018
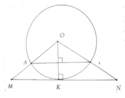
Tiếp tuyến MN, tiếp điểm K. Vì AB//MN
Nên OH ⊥ AB. Tính được OH = 3 5 R. Từ đó tính được KN = 4 3 R => S O M N = 4 3 R 2