Cho A = 1, B = \(\dfrac{1}{\sqrt{x}+3}\). Tìm x để A + B nhận giá trị nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2021
a: Thay \(x=\dfrac{1}{4}\) vào A, ta được:
\(A=\left(\dfrac{1}{2}+1\right):\left(\dfrac{1}{2}-2\right)=\dfrac{3}{2}:\dfrac{-3}{2}=-1\)
b: Ta có: \(B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\)
\(=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-12}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+4}{\sqrt{x}-2}\)
19 tháng 8 2021
c: Để B là số tự nhiên thì \(\sqrt{x}+4⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;2;3;6\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{3;4;5;8\right\}\)
hay \(x\in\left\{16;25;64\right\}\)
TL
2
8 tháng 4 2021
a,Ta có \(x=4-2\sqrt{3}=\sqrt{3}^2-2\sqrt{3}+1=\left(\sqrt{3}-1\right)^2\)
\(\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-1\right)^2}=\left|\sqrt{3}-1\right|=\sqrt{3}-1\)do \(\sqrt{3}-1>0\)
\(\Rightarrow A=\frac{1}{\sqrt{3}-1-1}=\frac{1}{\sqrt{3}-2}\)
b, Với \(x\ge0;x\ne1\)
\(B=\left(\frac{-3\sqrt{x}}{x\sqrt{x}-1}-\frac{1}{1-\sqrt{x}}\right):\left(1-\frac{x+2}{1+\sqrt{x}+x}\right)\)
\(=\left(\frac{-3\sqrt{x}+x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right):\left(\frac{x+\sqrt{x}+1-x-2}{x+\sqrt{x}+1}\right)\)
\(=\left(\frac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right):\left(\frac{\sqrt{x}-1}{x+\sqrt{x}+1}\right)\)
\(=\frac{\sqrt{x}-1}{x+\sqrt{x}+1}.\frac{x+\sqrt{x}+1}{\sqrt{x}-1}=1\)
Vậy biểu thức ko phụ thuộc biến x
c, Ta có : \(\frac{2A}{B}\)hay \(\frac{2}{\sqrt{x}-1}\)để biểu thức nhận giá trị nguyên
thì \(\sqrt{x}-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| \(\sqrt{x}-1\) | 1 | -1 | 2 | -2 |
| \(\sqrt{x}\) | 2 | 0 | 3 | -1 |
| x | 4 | 0 | 9 | vô lí |
TM
6 tháng 8 2023
(a) Với \(x\ge0,x\ne4\), ta có:
\(A=\dfrac{2x-3\sqrt{x}-2}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)\left(2\sqrt{x}+1\right)}{\sqrt{x}-2}=2\sqrt{x}+1\)
Để \(A\le5\Rightarrow2\sqrt{x}+1\le5\)
\(\Leftrightarrow2\sqrt{x}\le4\Leftrightarrow\sqrt{x}\le2\Leftrightarrow0\le x\le4\).
Kết hợp với điều kiện thì: \(0\le x< 4.\)
(b) \(\dfrac{A}{2}=\dfrac{2\sqrt{x}+1}{2}\) nguyên khi \(\left(2\sqrt{x}+1\right)\in B\left(2\right)=\left\{0;2;4;...;2n\right\}\left(n\in N\right)\)
\(\Leftrightarrow\sqrt{x}\in\left\{-\dfrac{1}{2};\dfrac{1}{2};\dfrac{3}{2};...;\dfrac{2n+1}{2}\right\}\left(n\in N\right)\)
Hay: \(\sqrt{x}\in\left\{\dfrac{1}{2};\dfrac{3}{2};...;\dfrac{2n+1}{2}\right\}\)
\(\Leftrightarrow x\in\left\{\dfrac{1}{4};\dfrac{9}{4};...;\dfrac{\left(2n+1\right)^2}{4}\right\}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
19 tháng 7 2023
\(B=\left[\dfrac{\sqrt{x-2}}{\left(\sqrt{x}-1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right]\sqrt{x}\left(\sqrt{x}-1\right)=\)
\(=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}\right]\sqrt{x}\left(\sqrt{x}-1\right)=\)
\(=\left[\dfrac{x+\sqrt{x}-2\sqrt{x}-2-x+\sqrt{x}-2\sqrt{x}+2}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}\right]\sqrt{x}\left(\sqrt{x}-1\right)=\)
\(=\left[\dfrac{-2\sqrt{x}}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}\right]\sqrt{x}\left(\sqrt{x}-1\right)=\)
\(=\dfrac{-2x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=-\dfrac{2x}{x-1}\)
b/
\(B=-\dfrac{2\left(x-1\right)+2}{x-1}=-2+\dfrac{2}{x-1}\)
Để B nguyên
\(x-1=\left\{-1;-2;1;2\right\}\Rightarrow x=\left[0;-1;2;3\right]\)
18 tháng 10 2021
a: Thay x=36 vào B, ta được:
\(B=\dfrac{6}{6-3}=\dfrac{6}{3}=2\)
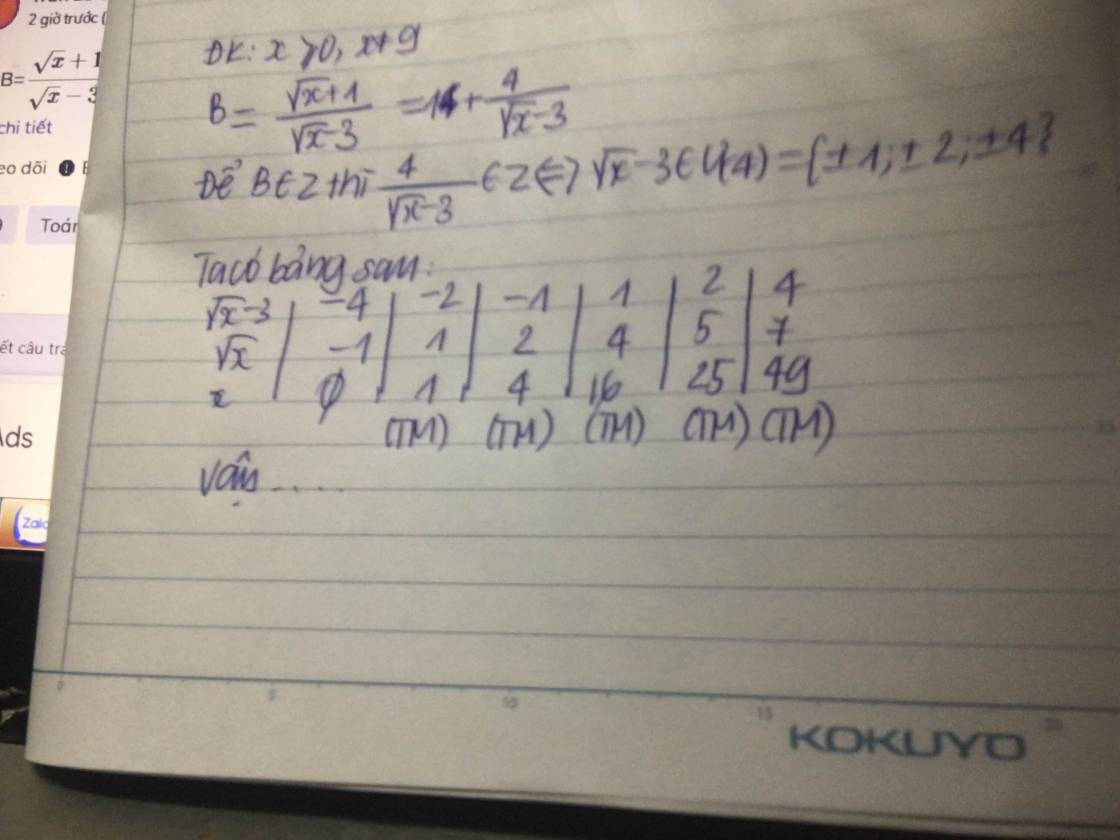
\(A+B=1+\dfrac{1}{\sqrt{x}+3}\left(đk:x\ge0\right)\)
Để A+B nhận giá trị nguyên thì: \(\sqrt{x}+3\inƯ\left(1\right)=\left\{1;-1\right\}\)
Vì \(x\ge0\)
\(\Rightarrow x\in\varnothing\)
Để A+B là số nguyên thì \(\sqrt{x}+4⋮\sqrt{x}+3\)
\(\Leftrightarrow\sqrt{x}+3\in\left\{1;-1\right\}\)(vô lý)