Cho hs y= x^4 - 2x^2 +2 . Diện tích S của tam giác có 3 đỉnh là 3 điểm cực trị của đồ thị hàm số đã cho có giá trị là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 9 2018
Đáp án C
Ta có y ' = 4 x 3 − 4 x ; y ' = 0 ⇔ x = 0 ⇒ y 0 = 2 x = ± 1 ⇒ y ± 1 = 1
Suy ra 3 điểm cực trị của ĐTHS là A 0 ; 2 , B 1 ; 1 , C − 1 ; 1
Khi đó A B = A C = 2 , B C = 2 ⇒ S Δ A B C = 1 2 A B 2 = 2 2 2 = 1
CM
28 tháng 7 2017
Đáp án C
Ta có: y’ = 8x3 – 8x
ð y’ = 0 ó x = 0 hoặc x = 1 hoặc x = -1
Ta có bảng biến thiên:
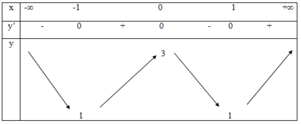
Vậy các điểm cực trị của hàm là: (-1;1), (0;3) và (1;1)
Theo công thức tính diện tích tam giác, ta có:
S = p ( p − a ) ( p − b ) ( p − c )
Trong đó
p = a + b + c 2
Vậy diện tích tam giác tạo bởi 3 điểm cực trị của đồ thị hàm số là 2
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(y'=4x^3-4mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=m\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A; B; C với \(\left\{{}\begin{matrix}A\left(0;m^4+2m\right)\\B\left(\sqrt{m};2m\right)\\C\left(-\sqrt{m};2m\right)\end{matrix}\right.\)
Tam giác ABC luôn cân tại A, gọi H là trung điểm BC \(\Rightarrow H\left(0;2m\right)\)
\(AH=\left|y_A-y_H\right|=m^4\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{m}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.m^4.2\sqrt{m}=4\)
\(\Leftrightarrow m^9=16\Rightarrow m=\sqrt[3]{2}\)
CM
6 tháng 7 2017
Chọn A
Ta có: y = 1 4 x 4 - 2 x 2 + 3
Các điểm cực trị: A ( - 2 ; - 1 ) ; B ( 0 ; 3 ) ; C ( 2 ; - 1 )
Các điểm cực trị tạo thành tam giác cân tại B H ( 0 ; - 1 ) là trung điểm của AC
Nên S ∆ A B C = 1 2 B H . A C = 8
CM
15 tháng 7 2017
Đáp án D
Có f ' x = 8 x 3 − 8 x ; f ' x = 0 ⇔ x = 0 x = 1 x = − 1
Từ đó 3 điểm cực trị là A − 1 ; 1 ; B 0 ; 3 ; C 1 ; 1 .
Nhận thấy rằng A B C là tam giác cân tại B với đường cao là BM , M là trung điểm của AC.
Tinh được A C = 2 ; B M = 2 ⇒ S A B C = 1 2 .2.2 = 2 .
CM
20 tháng 9 2019
Đáp án D
Ta có: y = f ' x = 4 x 3 − 4 x = 4 x x 2 − 1 ⇔ x = 0 x = ± 1
=> Các điểm cực trị là A 0 ; 3 , B 1 ; 2 , C − 1 ; 2 ⇒ Δ A B C cân tại
A ; B C = 1 + 1 2 + 2 − 2 2 = 2
Gọi I là trung điểm của B C ⇒ I 0 ; 2 ⇒ A I = h = 1
Ta có: S = 1 2 A I . B C = 1
Cách 2: Áp dụng CT giải nhanh: S = b 2 4 a . − b 2 a = 1
CM
9 tháng 3 2017
Đáp án D
Ta có
y ' = 4 x 3 − 4 x = 0 ⇔ x = 0 ⇒ y = 3 ⇒ A 0 ; 3 x = ± 1 ⇒ y = 2 ⇒ B 1 ; 2 , C − 1 ; 2
⇒ A B → = − 2 ; 0 ⇒ B C = 2 B C : y = 2 ⇒ d A ; B C = 1 ⇒ S A B C = 1 2 B C . d A ; B C = 1
\(y'=4x^3-4x=0\Rightarrow\left\{{}\begin{matrix}x=0\Rightarrow y=2\\x=1\Rightarrow y=1\\x=-1\Rightarrow y=1\end{matrix}\right.\)
\(S=\dfrac{1}{2}.\left(2-1\right)\left(1-\left(-1\right)\right)=1\)