Giúp mình giải câu 26 với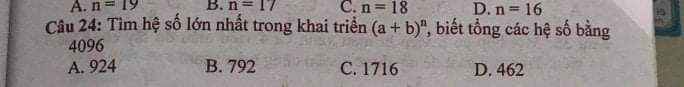
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2021
31 - [ 26 - ( 209 + 35 ) ]
= 31 - ( 26 - 344 )
=31 - ( -318)
= 31 + 318 ( trừ trừ thành cộng nha )
= 349
22 tháng 7 2021
31-(26-(209+35)=31-
hok tốt
k cho mik
kb nữa nhé
SV
Sinh Viên NEU
CTVVIP
6 tháng 10 2023
1 It was silly to lend him money
2 Meeting the president is exciting
3 While we were on the summer holiday, we were so happy
4 While they were playing, they cried twice
5 Writing good composition in English was not easy
3 tháng 10 2023
26 It was silly to lend him money
27 Meeting the president is exciting
28 While we were in the summer holiday, we were happy
29 While the play was being played, they cried twice
30 Writing good compositions in English was not easy
NV
10
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
18.
Áp dụng BĐT quen thuộc: \(\dfrac{1}{1+x^2}+\dfrac{1}{1+y^2}\ge\dfrac{2}{1+xy}\) ta có:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}\ge\dfrac{2}{1+\sqrt{a^3b^3}}\) ; \(\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{2}{1+\sqrt{abc^4}}\)
Cộng vế:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge2\left(\dfrac{1}{1+\sqrt{a^3b^3}}+\dfrac{1}{1+\sqrt{abc^4}}\right)\ge2\left(\dfrac{2}{1+\sqrt[4]{a^4b^4c^4}}\right)\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{4}{1+abc}\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}\ge\dfrac{3}{1+abc}\) (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
19.
Biến đổi tương đương:
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2+2ab\right)xy\)
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2\right)xy+2abxy\)
\(\Leftrightarrow ab\left(x^2+y^2\right)-2abxy\ge0\)
\(\Leftrightarrow ab\left(x^2+y^2-2xy\right)\ge0\)
\(\Leftrightarrow ab\left(x-y\right)^2\ge0\)
26 tháng 3 2022
Đặt \(\sqrt{\dfrac{x^2}{x-3}}=a\left(a>=0\right)\)
Theo đề, ta có bất phương trình:
\(a^2>2a+8\)
=>(a-4)(a+2)>0
=>a-4>0
\(\Leftrightarrow\dfrac{x^2}{x-3}>16\)
\(\Leftrightarrow x^2-16x+48>0\)
\(\Leftrightarrow x\in R\)
Vậy: S=R\{3}
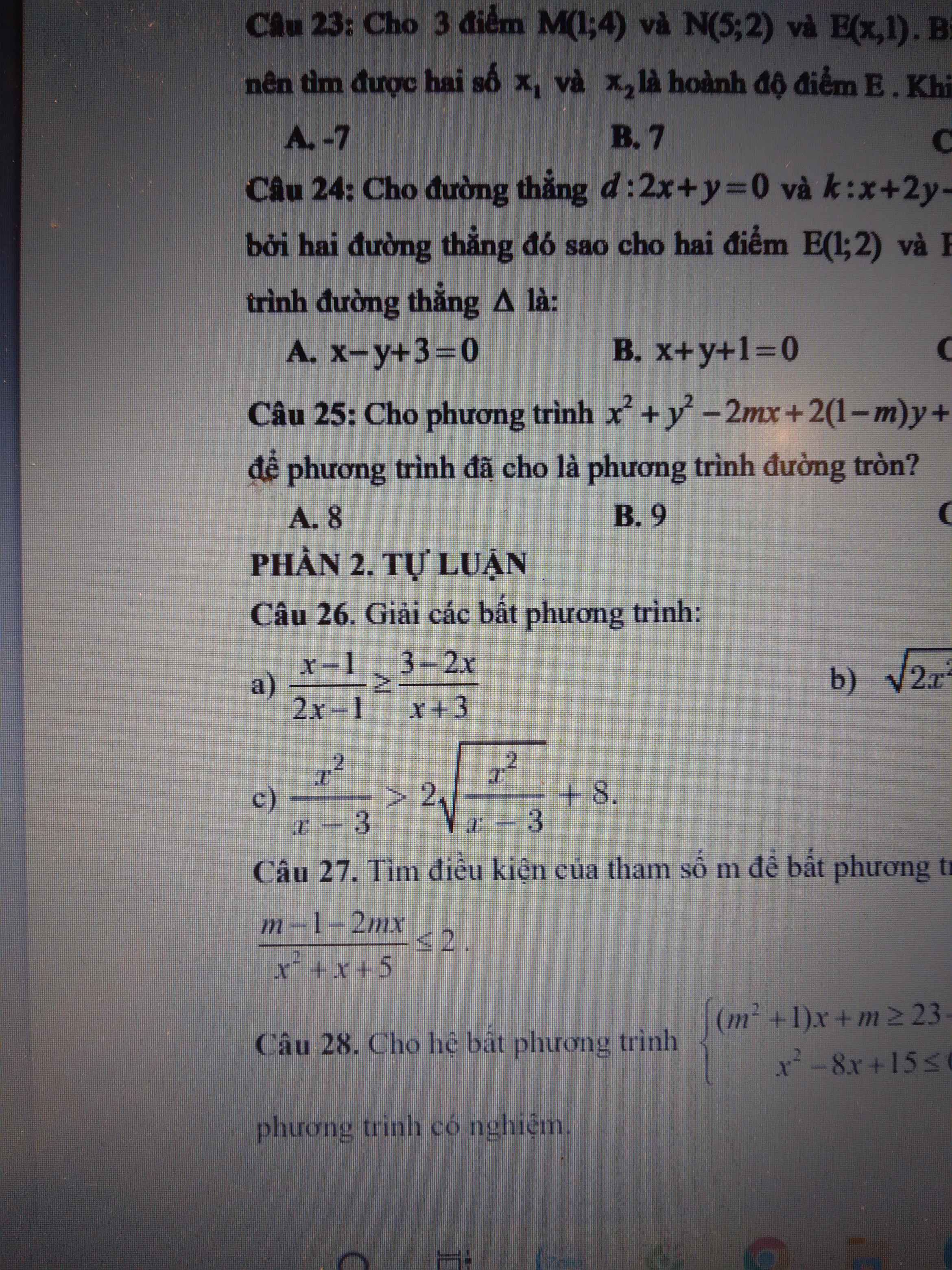
Ta có tổng hệ số của khai triển (a+b)^n là Cn0+C1n+....Cnn
theo đề ta có Cn0+C1n+....Cnn=4096=>(1+1)^n=4096=>2^n=4096=>n=12
vậy n=12
Xét Ck12>Ck+112=>k<11/2=>k=1,2,3,4,5
=>C112<C212<...<C512<C612>C712>.......>C1212
vậy k max =6=> hệ số lớn nhất trong khai triển:C126=924=>A
Chọn A