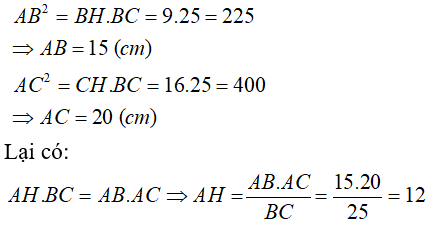Bài 9 với ah
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LN
Lê Nữ Khánh Huyền
28 tháng 11 2017
| Adjectives | Comparatives | Superatives |
| good | better | the best |
| loud | louder | |
| intelligent | more intelligent | the most intelligent |
| big | bigger | the biggest |
Đúng(0)
Những câu hỏi liên quan
19 tháng 8 2021
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=9\cdot25=225\\AC^2=16\cdot25=400\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
KT
10 tháng 7 2018
hình tự vẽ nhé:
Áp dụng hệ thức lượng ta có:
\(AC^2=HC.BC=9BC\)
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(400+9BC=BC^2\)
\(\Leftrightarrow\)\(BC^2-9BC-400=0\)
\(\Leftrightarrow\)\(\left(BC-25\right)\left(BC+16\right)=0\)
\(\Leftrightarrow\)\(BC=25\)
\(\Rightarrow\)\(AC^2=9.25=225\)
\(\Rightarrow\)\(AC=\sqrt{225}=15\)
Áp dụng hệ thức lượng ta có:
\(AB.AC=AH.BC\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}\)
\(\Rightarrow\)\(AH=\frac{20.15}{25}=12\)
14 tháng 6 2020
[ 48 phut 36 giay : 9 ] + 9,54 phut = 5phut 24 giay + 9,54 phut = 5,4 phut + 9,54 phut = 14,94 phut
20 tháng 5 2022
a: Xet ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó: ΔAHB\(\sim\)ΔBCD
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(AH=\dfrac{AB\cdot AD}{BD}=4,8\left(cm\right)\)
c: \(HB=\dfrac{AB^2}{BD}=6,4\left(cm\right)\)
\(S=\dfrac{AH\cdot HB}{2}=2,4\cdot6,4=15,36\left(cm^2\right)\)
N
2
12 tháng 9 2021
Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
11 tháng 7 2023
1:
Xét ΔABD và ΔACE có
AB=AC
góc B=góc C
BD=CE
=>ΔABD=ΔACE
=>AD=AE
2:
a: H là trung điểm của DB
=>D thuộc tia đối của tia HB
=>D thuộc HC
b: góc KCD=góc DAH
góc DAH=góc CED
=>góc KCD=góc CED
Xét ΔCED vuông tại E và ΔCKD vuông tại K có
CD chung
góc ECD=góc KCD
=>ΔCED=ΔCKD
=>DE=DK