Trong cùng hệ trục tọa độ Oxy cho ba điểm A(2;4), B(-3;-1), C(-2;1). Chứng minh ba điểm A,B,C không thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,\) PT hoành độ giao điểm: \(3x+2=x-2\Leftrightarrow x=-2\Leftrightarrow y=-4\Leftrightarrow A\left(-2;-4\right)\)
Vậy \(A\left(-2;-4\right)\) là tọa độ giao điểm

Chọn C.
Phương pháp:
Viết phương trình đường thẳng dưới dạng phương trình đoạn chắn.
Cách giải:
![]()

Đường thẳng OA có dạng y = ax
Vì \(A\in OA\Rightarrow2=a\)
\(\Rightarrow OA:y=2x\)
Để O;A;M thẳng hàng thì \(M\in OA\)
\(\Leftrightarrow m^2=2m\)
\(\Leftrightarrow m^2-2m=0\)
\(\Leftrightarrow m\left(m-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=0\\m=2\end{cases}}\)

1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
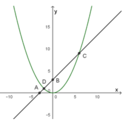
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .
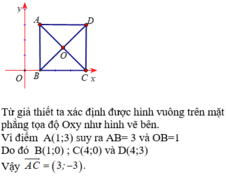

Ta có:
vt AB(Xb-Xa;Yb-Ya)=(-3-2;-1-4)=(-5;-5)
vt BC(Xc-Xb;Yc-Yb)=(-2+3;1+1)=(1;2)
vt CA(Xa-Xc;Ya-Yc)=(2+2;4-1)=(4;3)
vt AC(Xc-Xa;Yc-Ya)=(-2-2;1-4)=(-4;-3)
=>-5/-5 khác -4/-3 =>3 điểm A,B,C không thẳng hàng