Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên AD=AE
Ta có: AE+EB=AB
AD+DC=AC
mà AB=AC
và AD=AE
nên EB=DC
Xét ΔEBO vuông tại E và ΔDCO vuông tại D có
EB=DC
\(\widehat{EBO}=\widehat{DCO}\)
Do đó: ΔEBO=ΔDCO
c: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
DO đó:ΔABO=ΔACO
Suy ra: \(\widehat{BAO}=\widehat{CAO}\)
hay AO là tia phân giác của góc BAC
xét ΔADM và ΔADN có:
AD chung
MAD=NAD(góc)
AMD=AND=90(góc)
⇒ΔADM=ΔADN(cạnh huyền--góc nhọn)
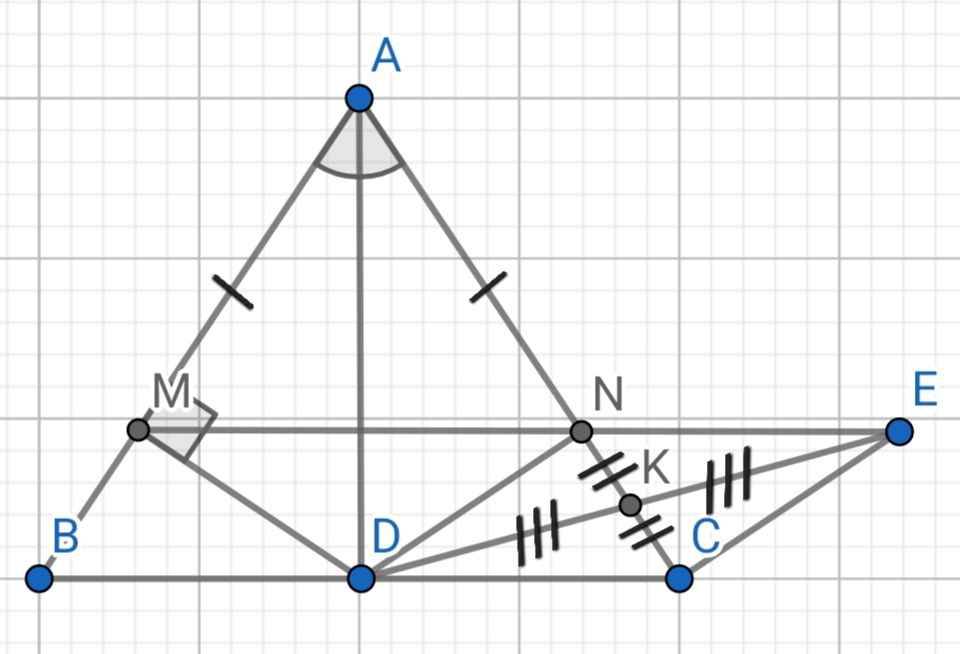a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng
