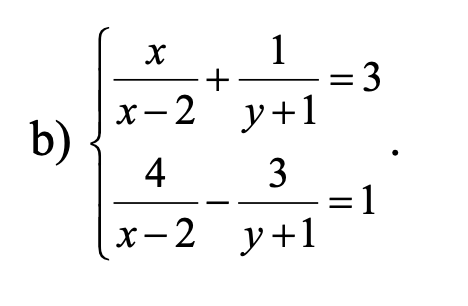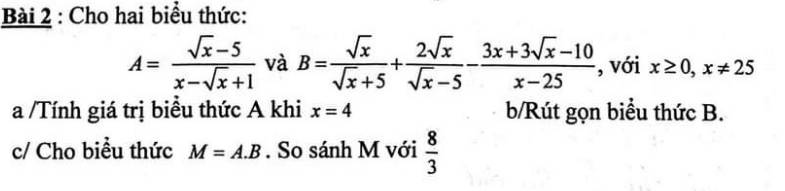Giải giúp em câu này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t


\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-2+2}{x-2}+\dfrac{1}{y+1}=3\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x-2}+\dfrac{3}{y+1}=6\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x-2}=7\\\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-2=\dfrac{10}{7}\\\dfrac{1}{y+1}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{24}{7}\\y=\dfrac{2}{3}\end{matrix}\right.\)

Vì \(\sqrt{3\sqrt{2\sqrt{x}}}\) là số nguyên => \(3\sqrt{2\sqrt{x}}\) là số chính phương.
Mà 3 là số nguyên tố nên \(\sqrt{2\sqrt{x}}\)có dạng \(3k^2\) với k ∈ N*
\(\sqrt{2\sqrt{x}}=3k^2\Leftrightarrow2\sqrt{x}=9k^4\Leftrightarrow4x=81k^8\)\(\Leftrightarrow x=\dfrac{81}{4}k^8\)
Vì x là số có 4 chữ số => \(x\le9999\) => \(\dfrac{81}{4}k^8\le9999\Leftrightarrow k^8\le\dfrac{4444}{9}\Leftrightarrow k^8\le493\) (1)
Vì \(k\ge1\) => \(k^8\ge1\) (2)
Từ (1) và (2), ta có \(k^8\in\left\{1,256\right\}\)
-Xét \(k^8=1\Rightarrow k=1\Rightarrow x=\)\(\dfrac{81}{4}\) => Vô lí
-Xét \(k^8=256\Rightarrow k=2\Rightarrow x=5184\) t/m
Vậy x = 5184


Do ABCD là hình thoi \(\Rightarrow\overrightarrow{AD}=\overrightarrow{BC}\), do M là trung điểm AB \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\)
Do đó:
\(\overrightarrow{MA}+\overrightarrow{MD}+2\overrightarrow{MC}=\overrightarrow{MA}+\left(\overrightarrow{MA}+\overrightarrow{AD}\right)+2\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(=2\left(\overrightarrow{MA}+\overrightarrow{MB}\right)+\overrightarrow{AD}+2\overrightarrow{BC}=\overrightarrow{BC}+2\overrightarrow{BC}=3\overrightarrow{BC}\)

a: Khi x=4 thì \(A=\dfrac{2-5}{4-2+1}=\dfrac{-3}{3}=-1\)
b: \(B=\dfrac{x-5\sqrt{x}+2x+10\sqrt{x}-3x-3\sqrt{x}+10}{x-25}\)
\(=\dfrac{2\sqrt{x}+10}{x-25}=\dfrac{2}{\sqrt{x}-5}\)

\(f\left(x\right)=ax^3+bx^2+cx+d\)
Dựa vào đồ thị ta có: \(f\left(-2\right)=2,f\left(-1\right)=-1,f\left(0\right)=0,f\left(1\right)=-1\)
Từ đó suy ra \(f\left(x\right)=-x^3-x^2+x\).
\(g\left(x\right)=\left|f^3\left(x\right)-3f\left(x\right)\right|\)
\(h\left(x\right)=f^3\left(x\right)-3f\left(x\right)\)
\(h'\left(x\right)=3f'\left(x\right)f^2\left(x\right)-3f'\left(x\right)\)
\(h'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f^2\left(x\right)=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f\left(x\right)=1\\f\left(x\right)=-1\end{matrix}\right.\)
\(f'\left(x\right)=0\) có \(2\) nghiệm đơn
\(f\left(x\right)=1\) có \(1\) nghiệm đơn
\(f\left(x\right)=-1\) có \(1\) nghiệm đơn, \(1\) nghiệm kép.
Kết hợp lại ta được phương trình \(h'\left(x\right)=0\) có \(4\) nghiệm bội lẻ (do nghiệm \(x=-1\) vừa là nghiệm kép của \(f\left(x\right)=-1\) vừa là nghiệm đơn của \(f'\left(x\right)=0\)).
mà \(limh\left(x\right)=-\infty\) do đó \(g\left(x\right)=\left|h\left(x\right)\right|\) có \(3\) điểm cực đại, \(4\) điểm cực tiểu suy ra \(T=n^m=4^3=64\).
Chọn A.

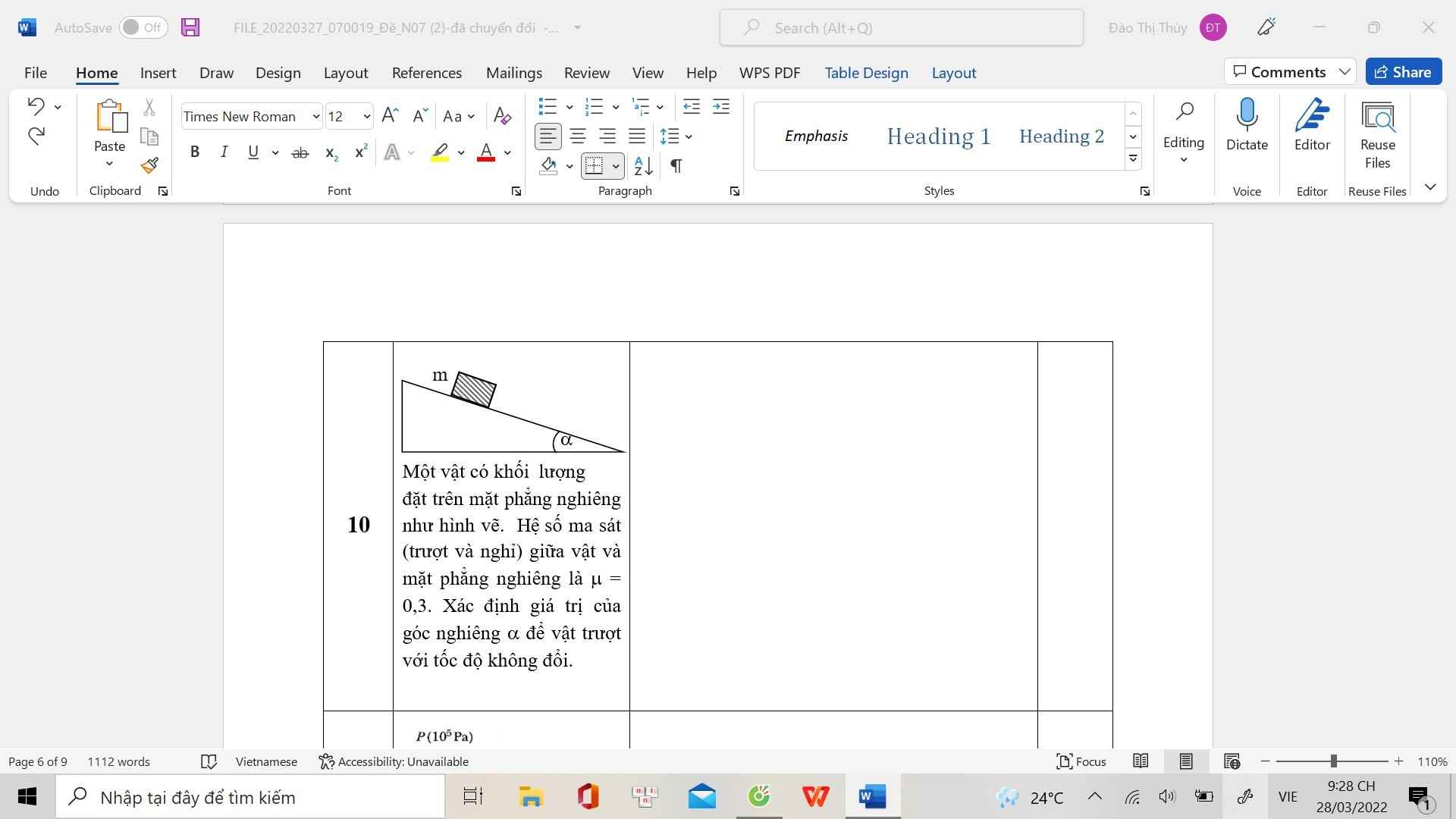
đề cho thiếu rồi em, đề có cho góc \(\alpha\) bằng bao nhiêu không em

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA
Ta có: CB\(\perp\)CA
OI\(\perp\)AC
Do đó: OI//CB
b: Xét ΔOAI vuông tại A có AH là đường cao
nên \(OH\cdot OI=OA^2=R^2\)
=>\(OH\cdot OI=OB^2\)
=>OH/OB=OB/OI
Xét ΔOHB và ΔOBI có
\(\dfrac{OH}{OB}=\dfrac{OB}{OI}\)
\(\widehat{HOB}\) chung
Do đó: ΔOHB đồng dạng với ΔOBI
=>\(\widehat{OBH}=\widehat{OIB}\)