
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-2+2}{x-2}+\dfrac{1}{y+1}=3\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x-2}+\dfrac{3}{y+1}=6\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x-2}=7\\\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-2=\dfrac{10}{7}\\\dfrac{1}{y+1}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{24}{7}\\y=\dfrac{2}{3}\end{matrix}\right.\)

Vì \(\sqrt{3\sqrt{2\sqrt{x}}}\) là số nguyên => \(3\sqrt{2\sqrt{x}}\) là số chính phương.
Mà 3 là số nguyên tố nên \(\sqrt{2\sqrt{x}}\)có dạng \(3k^2\) với k ∈ N*
\(\sqrt{2\sqrt{x}}=3k^2\Leftrightarrow2\sqrt{x}=9k^4\Leftrightarrow4x=81k^8\)\(\Leftrightarrow x=\dfrac{81}{4}k^8\)
Vì x là số có 4 chữ số => \(x\le9999\) => \(\dfrac{81}{4}k^8\le9999\Leftrightarrow k^8\le\dfrac{4444}{9}\Leftrightarrow k^8\le493\) (1)
Vì \(k\ge1\) => \(k^8\ge1\) (2)
Từ (1) và (2), ta có \(k^8\in\left\{1,256\right\}\)
-Xét \(k^8=1\Rightarrow k=1\Rightarrow x=\)\(\dfrac{81}{4}\) => Vô lí
-Xét \(k^8=256\Rightarrow k=2\Rightarrow x=5184\) t/m
Vậy x = 5184

a: Khi x=4 thì \(A=\dfrac{2-5}{4-2+1}=\dfrac{-3}{3}=-1\)
b: \(B=\dfrac{x-5\sqrt{x}+2x+10\sqrt{x}-3x-3\sqrt{x}+10}{x-25}\)
\(=\dfrac{2\sqrt{x}+10}{x-25}=\dfrac{2}{\sqrt{x}-5}\)


\(a,=7\cdot6+15:5=42+3=45\\ b,=6+3\sqrt{5}-6=3\sqrt{5}\)

b: \(=\dfrac{2}{\sqrt{x}-2}:\dfrac{\sqrt{x}+\sqrt{x}+2}{x-4}\)
\(=\dfrac{2}{\sqrt{x}-2}\cdot\dfrac{x-4}{2\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)

4: \(x^2-2\left(m+1\right)x+m-4=0\left(1\right)\)
Thay m=1 vào phương trình (1), ta được:
\(x^2-2\cdot\left(1+1\right)x+1-4=0\)
=>\(x^2-4x-3=0\)
=>\(x^2-4x+4-7=0\)
=>\(\left(x-2\right)^2=7\)
=>\(x-2=\pm\sqrt{7}\)
=>\(x=2\pm\sqrt{7}\)
5: Để phương trình (1) có hai nghiệm trái dấu thì \(1\cdot\left(m-4\right)< 0\)
=>m-4<0
=>m<4
6: \(\text{Δ}=\left(-2m-2\right)^2-4\left(m-4\right)\)
\(=4m^2+8m+4-4m+16\)
\(=4m^2+4m+20\)
\(=4m^2+4m+1+19=\left(2m+1\right)^2+19>0\forall m\)
=>Phương trình (1) luôn có hai nghiệm phân biệt
Áp dụng định lí Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=2\left(m+1\right)\\x_1\cdot x_2=\dfrac{c}{a}=m-4\end{matrix}\right.\)
\(A=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}\)
\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(2m+2\right)^2-4\left(m-4\right)}\)
\(=\sqrt{4m^2+8m+4-4m+16}\)
\(=\sqrt{4m^2+4m+1+19}\)
\(=\sqrt{\left(2m+1\right)^2+19}>=\sqrt{19}\forall m\)
Dấu '=' xảy ra khi 2m+1=0
=>2m=-1
=>\(m=-\dfrac{1}{2}\)
Vậy: \(A_{min}=\sqrt{19}\) khi \(m=-\dfrac{1}{2}\)

Câu 1:
1:
a: \(\dfrac{1}{2}x-3=0\)
=>\(\dfrac{1}{2}x=3\)
=>\(x=3:\dfrac{1}{2}=3\cdot2=6\)
b: \(3x^2-12x=0\)
=>\(3x\cdot x-3x\cdot4=0\)
=>\(3x\left(x-4\right)=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
2:
a: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=-x+\dfrac{3}{2}\)
=>\(x^2=-2x+3\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Khi x=-3 thì \(y=\dfrac{1}{2}\cdot\left(-3\right)^2=\dfrac{1}{2}\cdot9=4,5\)
Khi x=1 thì \(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)
b: Gọi (d1): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Thay x=2 và y=2 vào (d), ta được:
\(a\cdot2+b=2\)
=>2a+b=2
=>b=2-2a
=>y=ax+2-2a
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=ax+2-2a\)
=>\(\dfrac{1}{2}x^2-ax-2+2a=0\)
\(\text{Δ}=\left(-a\right)^2-4\cdot\dfrac{1}{2}\cdot\left(2a-2\right)\)
\(=a^2-2\left(2a-2\right)=a^2-4a+4=\left(a-2\right)^2\)
Để (P) tiếp xúc với (d1) thì Δ=0
=>a-2=0
=>a=2
=>b=2-2a=2-4=-2
Vậy: Phương trình đường thẳng cần tìm là y=2x-2
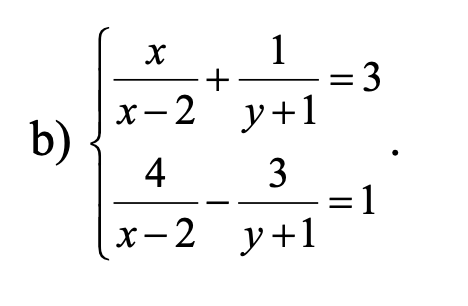

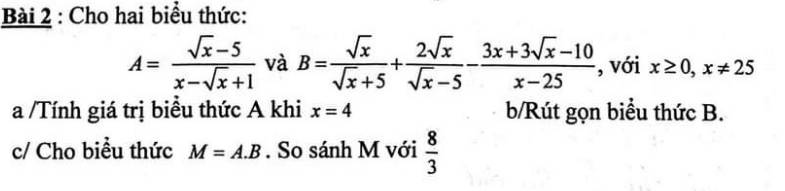

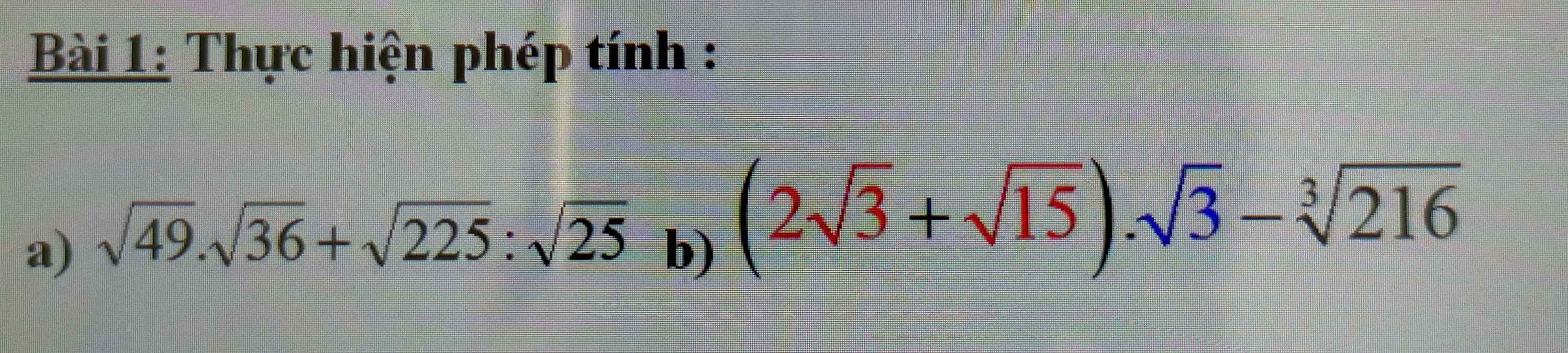 giải giúp em 2 câu này với ạ
giải giúp em 2 câu này với ạ 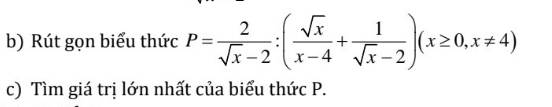
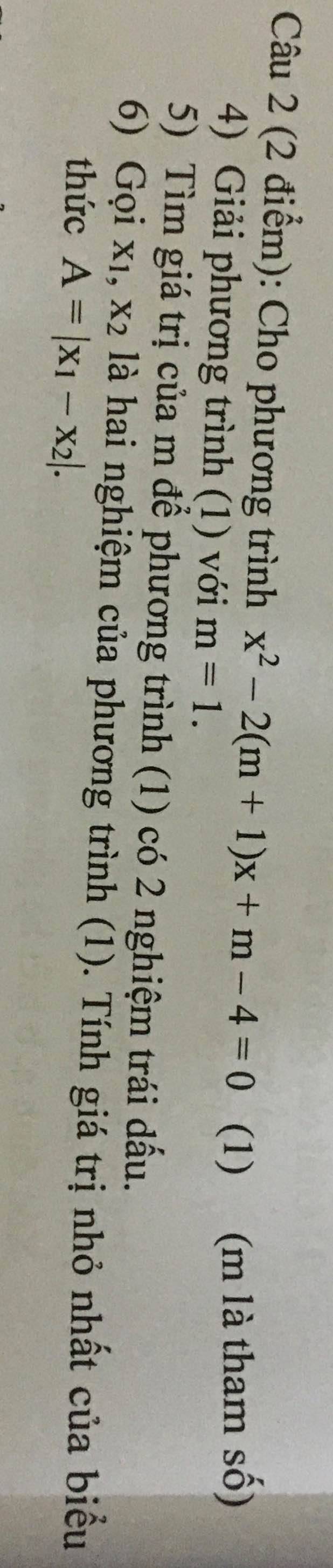


a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA
Ta có: CB\(\perp\)CA
OI\(\perp\)AC
Do đó: OI//CB
b: Xét ΔOAI vuông tại A có AH là đường cao
nên \(OH\cdot OI=OA^2=R^2\)
=>\(OH\cdot OI=OB^2\)
=>OH/OB=OB/OI
Xét ΔOHB và ΔOBI có
\(\dfrac{OH}{OB}=\dfrac{OB}{OI}\)
\(\widehat{HOB}\) chung
Do đó: ΔOHB đồng dạng với ΔOBI
=>\(\widehat{OBH}=\widehat{OIB}\)