cho hình vẽ biết bm //cn tinh bac
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Vì MB//CN\(\Rightarrow\widehat{ACN}=\widehat{CAx}\)(2 góc so le trong)
mà \(\widehat{ACN}=55^0\)
\(\Rightarrow\widehat{CAx}=55^0\)
b, Theo bài ra ta có :\(\widehat{BAC}\)=\(\widehat{CAx}+\widehat{BAx}\)
\(\Rightarrow108^0=55^0+\widehat{BAx}\Rightarrow\widehat{BAx}=53^0\)
mà\(\widehat{BAx}=\widehat{ABM}\)(2 góc so le trong)
\(\widehat{BAx}=53^0\Rightarrow\widehat{ABM}=53^0\)
Vậy\(\widehat{CAx}=55^0\)
\(\widehat{ABM}=53^0\)


Nhìn bên phải, bấm vô thống kê hỏi đáp ạ, VÀO TRANG CÁ NHÂN CỦA E Em bức xúc lắm anh chị ạ, xl mấy anh chị vì đã gây rối Thiệt tình là ko chấp nhận nổi con nít ms 2k6 mà đã là vk là ck r ạ, bày đặt yêu xa, chưa lên đại học Đây là \'tội nhân\' https://olm.vn/thanhv



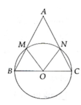
a, Chứng minh được ∆BOM = ∆CON (c.g.c) từ đó suy ra B M ⏜ = C N ⏜
b, Tính được M O N ^ = 100 0

Mình xin sửa lại đề một chút
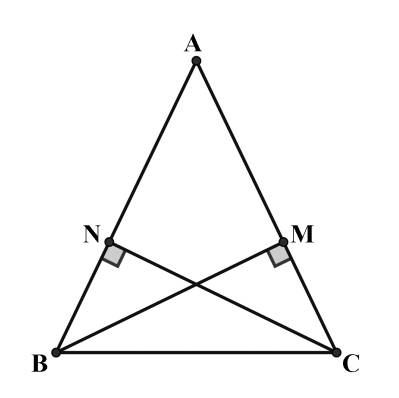
Bài 3: Cho ΔABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BM=CN. Vẽ BD⊥AM tại D và CE⊥AN tại E.
a) Cm ΔAMN cân
b) Cm DB=CE
Bài làm:
a) Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACN}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
Suy ra: AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
b) Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BM=CN(gt)
\(\widehat{M}=\widehat{N}\)(ΔABM=ΔACN)
Do đó: ΔMBD=ΔNCE(Cạnh huyền-góc nhọn)
Suy ra: DB=EC(Hai cạnh tương ứng)


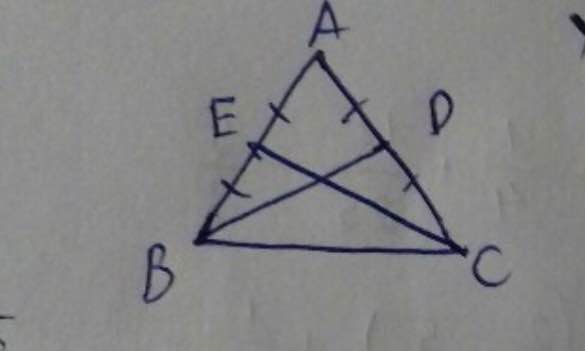
sai đề bạn ơi
à mình nhầm