Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\Delta CAN:A_1+C=90\Rightarrow C=90-A_1\)
\(A_2=90-A_1=90-\left(90-C\right)=C\)
Tam giác vuông ABM và tam giác vuông CAN: AB = AC ; A2^ = C^ => Tam giác ABM = tam giác CAN (cạnh huyền_góc nhọn) (1)
b) Từ (1) => AM = CN và BM = AN (2 cạnh tương ứng) (*)
Ta có: BM = AN + AM (**)
Từ (*) và (**) => MN = BM + CN
c) Tam giác vuông ABC cân tại A (do AB = AC) => ABC^ = ACB^ = 45o
Mình chưa học tam giác cân rùi còn cách nào khác ko bạn

Tam giác NAC vuông tại N có:
NAC + NCA = 900
NAC = 900 - NCA
Ta có:
MAB + BAC + CAN = MAN
MAB + 900 + 900 - NCA = 1800
MAB = 1800 - 900 - 900 + NCA
MAB = NCA
Xét tam giác MAB vuông tại M và tam giác NCA vuông tại N có:
AB = AC (gt)
MAB = NCA (chứng minh trên)
=> Tam giác MAB = Tam giác NCA (cạnh huyền - góc nhọn)
=> MA = NC (2 cạnh tương ứng)
AN = BM (2 cạnh tương ứng)
=> MA + AN = NC + BM
hay MN = NC + BM
Tam giác ABC vuông tại A
mà AB = AC (gt)
=> Tam giác ABC vuông cân tại A
=> ABC = ACB = 450

Tam giác NAC vuông tại N có:
NAC + NCA = 900
NAC = 900 - NCA
Ta có:
MAB + BAC + CAN = MAN
MAB + 900 + 900 - NCA = 1800
MAB = 1800 - 900 - 900 + NCA
MAB = NCA
Xét tam giác MAB vuông tại M và tam giác NCA vuông tại N có:
AB = AC (gt)
MAB = NCA (chứng minh trên)
=> Tam giác MAB = Tam giác NCA (cạnh huyền - góc nhọn)
=> MA = NC (2 cạnh tương ứng)
AN = BM (2 cạnh tương ứng)
=> MA + AN = NC + BM
hay MN = NC + BM
Tam giác ABC vuông tại A
mà AB = AC (gt)
=> Tam giác ABC vuông cân tại A
=> ABC = ACB = 450

a: XétΔABC có
BM là đường cao
CN là đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
Suy ra: AH vuông góc với BC
b: \(\widehat{MHN}=360^0-90^0-90^0-70^0=110^0\)
=>\(\widehat{BHN}=70^0\)

a: BD+BC=DC
BC+CE=BE
mà BD=CE
nên DC=BE
Xét ΔABE và ΔACD có
AE=AD
\(\widehat{E}=\widehat{D}\)
BE=CD
Do đó: ΔABE=ΔACD
=>\(\widehat{ABC}=\widehat{ACB}\)
=>AB=AC
b: Xét ΔABD và ΔACE có
AB=AC
BD=CE
AD=AE
Do đó: ΔABD=ΔACE
=>\(\widehat{BAD}=\widehat{CAE}\)
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
\(\widehat{BAM}=\widehat{CAN}\)
Do đó: ΔAMB=ΔANC
=>BM=CN
c: Xét ΔMBD vuông tại M và ΔNCE vuông tại N có
BD=CE
MB=NC
Do đó: ΔMBD=ΔNCE
=>\(\widehat{MBD}=\widehat{NCE}\)
mà \(\widehat{IBC}=\widehat{MBD}\)(hai góc đối đỉnh)
và \(\widehat{NCE}=\widehat{ICB}\)(hai góc đối đỉnh)
nên \(\widehat{ICB}=\widehat{IBC}\)
=>IB=IC
Xét ΔABI và ΔACI có
AB=AC
IB=IC
AI chung
Do đó: ΔABI=ΔACI
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của góc BAC

1: Ta có: ΔABC cân tại A
nên \(\widehat{ABC}=\widehat{ACB}\)
2: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{BAD}\) chung
AD=AE
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
3: Xét tứ giác ABCM có
D là trung điểm của AC
D là trung điểm của BM
Do đó:ABCM là hình bình hành
Suy ra: AM//BC và AM=BC
Xét tứ giác ACBN có
E là trung điểm của AB
E là trung điểm của CN
Do đó:ACBN là hình bình hành
Suy ra: AN//BC và AN=BC
Ta có: AM//BC
AN//BC
mà AM,AN có điểm chung là A
nên M,A,N thẳng hàng
mà AM=AN(=BC)
nên A là trung điểm của MN
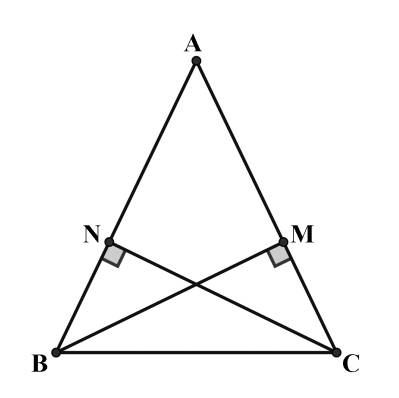
- Xét △BNC và △CMB có:
\(\widehat{BNC}=\widehat{CMB}=90^0\)
\(CN=BM\left(gt\right)\)
\(BC\) chung
⇒ △BNC = △CMB (ch - cgv)
⇒ \(\widehat{ABC}=\widehat{ACB}\left(đpcm\right)\)