Phương trình \(2sin^2x-4sinxcosx+4cos^2x=1\) có phương trình tương đương là?
Giúp mk vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2022
a, để pt trên là pt bậc nhất khi m khác 2
b, Ta có \(2x+5=x+7-1\Leftrightarrow x=1\)
Thay x = 1 vào pt (1) ta được
\(2\left(m-2\right)+3=m-5\Leftrightarrow2m-1=m-5\Leftrightarrow m=-4\)
PT
Bất phương trình x > 3 và bất phương trình 6 < 2x có phải là hai bất phương trình tương đương không?
1
CM
6 tháng 1 2018
Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.
Do bất phương trình x > 3 và bất phương trình 6 < 2x có cùng tập nghiệm là { x| x > 3 } nên hai bất phương trình này là hai bất phương trình tương đương
HH
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
\(\Leftrightarrow2sin^3x+1-sin^2x-1=0\)
\(\Leftrightarrow sin^2x\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
PT
1
CM
22 tháng 7 2017
Đáp án: C
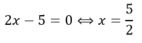
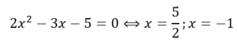
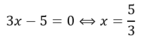
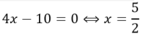
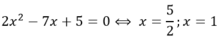
Ta thấy phương trình 
có cùng tập nghiệm với phương trình 
nên 2 phương trình là tương đương.
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Lời giải:
a/
PT $(1)$ có nghiệm $x=\frac{2}{3}$. PT $(2)$ có nghiệm $x=\frac{3}{2}$
Cộng 2 vế tương ứng của pt đã cho thì có:
$5x=5\Leftrightarrow x=1$
Vậy tập nghiệm của pt sau không giống 2 pt đầu nên câu trả lời là không.
b.
PT đó không phải hệ quả của 1 trong 2 PT ban đầu vì \(\left\{\frac{2}{3}\right\}\not\subset\left\{1\right\}; \left\{\frac{3}{2}\right\}\not\subset\left\{1\right\}\)
LA
25 tháng 3 2017
a) Phương trình bậc nhất một ẩn là phương trình 2x -8 = 0
b) Hai phương trình tương đương là hai phương trình có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = {-2/3}
25 tháng 3 2017
a) Phương trình bậc nhất một ẩn là phương trình :
2x - 8 = 0
b) Hai phương trình tương đương với nhau vì chúng có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = ( -2 / 3 )
ai tk mk mk tk lại!!
TH1: Xét cox = 0 ( có p là nghiệm ko)
TH2: Xét \(\cos x\ne0\). Ta chia cả hai vế \(\cos^2x\)
Pt trở thành \(2\tan^2x-4\tan x+4-1\left(1+\tan^2x\right)=0\)
\(\Leftrightarrow\tan^2x-4\tan x+3=0\)
Đặt \(\tan x=t\). Giải pt nữa là xg ạ
\(2sin^2x-4sinx.cosx+4cos^2x=1\)
\(\Leftrightarrow2\left(sin^2x+cos^2x\right)-4sinx.cosx+2cos^2x-1=0\)
\(\Leftrightarrow2-2sin2x+cos2x=0\)
\(\Leftrightarrow2sin2x-cos2x=2\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sin2x-\dfrac{1}{\sqrt{5}}cos2x\right)=2\)
\(\Leftrightarrow sin\left(2x-arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{2}{\sqrt{5}}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-arccos\dfrac{2}{\sqrt{5}}=arcsin\dfrac{2}{\sqrt{5}}+k2\pi\\2x-arccos\dfrac{2}{\sqrt{5}}=\pi-arcsin\dfrac{2}{\sqrt{5}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}arccos\dfrac{2}{\sqrt{5}}+\dfrac{1}{2}arcsin\dfrac{2}{\sqrt{5}}+k\pi\\x=\dfrac{\pi}{2}+\dfrac{1}{2}arccos\dfrac{2}{\sqrt{5}}-\dfrac{1}{2}arcsin\dfrac{2}{\sqrt{5}}+k\pi\end{matrix}\right.\)