Cho 2x + 3y = 5 . Tìm Min của F = 2x2 + 3y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VH
7 tháng 10 2015
2x+3y=5
=>x=\(\frac{5-3x}{2}\)
=>F=\(2.\frac{\left(5-3y\right)^2}{4}+3y^2=\frac{25-30y+9y^2}{2}+\frac{6y^2}{2}\)
\(=\frac{25-30y+15y^2}{2}=\frac{15y^2-30y+15+10}{2}\)
\(=\frac{15.\left(y-1\right)^2+10}{2}=\frac{15.\left(y-1\right)^2}{2}+5\ge5\)
Dấu "=" xảy ra khi : y=1 =>x=\(\frac{5-3}{2}=1\)
kakaka bik giải rùi
5 tháng 10 2021
\(A=\left(2x-1\right)^2+9\ge9\\ A_{min}=9\Leftrightarrow x=\dfrac{1}{2}\\ B=2\left(x^2-2\cdot\dfrac{3}{4}x+\dfrac{9}{16}\right)+\dfrac{1}{8}=2\left(x-\dfrac{3}{4}\right)^2+\dfrac{1}{8}\ge\dfrac{1}{8}\\ B_{min}=\dfrac{1}{8}\Leftrightarrow x=\dfrac{3}{4}\\ C=\left(4x^2+4xy+y^2\right)+2\left(2x+y\right)+1+\left(y^2+4y+4\right)-4\\ C=\left[\left(2x+y\right)^2+2\left(2x+y\right)+1\right]+\left(y+2\right)^2-4\\ C=\left(2x+y+1\right)^2+\left(y+2\right)^2-4\ge-4\\ C_{min}=-4\Leftrightarrow\left\{{}\begin{matrix}2x=-1-y\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=-2\end{matrix}\right.\)
\(D=\left(3x-1-2x\right)^2=\left(x-1\right)^2\ge0\\ D_{min}=0\Leftrightarrow x=1\\ G=\left(9x^2+6xy+y^2\right)+\left(y^2+4y+4\right)+1\\ G=\left(3x+y\right)^2+\left(y+2\right)^2+1\ge1\\ G_{min}=1\Leftrightarrow\left\{{}\begin{matrix}3x=-y\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-2\end{matrix}\right.\)
5 tháng 10 2021
\(H=\left(x^2-2xy+y^2\right)+\left(x^2+2x+1\right)+\left(2y^2+4y+2\right)+2\\ H=\left(x-y\right)^2+\left(x+1\right)^2+2\left(y+1\right)^2+2\ge2\\ H_{min}=2\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=-1\\y=-1\end{matrix}\right.\Leftrightarrow x=y=-1\)
Ta luôn có \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2xz\ge0\\ \Leftrightarrow x^2+y^2+z^2\ge xy+yz+xz\\ \Leftrightarrow x^2+y^2+z^2+2xy+2yz+2xz\ge3xy+3yz+3xz\\ \Leftrightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+xz\right)\\ \Leftrightarrow\dfrac{3^2}{3}\ge xy+yz+xz\\ \Leftrightarrow K\le3\\ K_{max}=3\Leftrightarrow x=y=z=1\)
CM
17 tháng 4 2017
Có hai cách trình bày với bài này: một là bạn có thể liệt kê hết các phần tử ra hoặc bạn sắp xếp theo cùng thứ tự và tính như sau:
20 tháng 5 2022
Mình tính thẳng ra nhé.
a) -A+B-C= -4x^2 + 2xy - 3y^2 + 3y + 7.
b) A+B-(-C)= -5y^2 = 2xy - 4x + 9y + 5.
HN
2
H9
HT.Phong (9A5)
CTVHS
27 tháng 7 2023
Ta có:
\(2x+y=11z\) và \(3x-y=4z\)
Chia theo vế ta có:
\(\dfrac{2x+y}{3x-y}=\dfrac{11z}{4z}=\dfrac{11}{4}\)
\(\Leftrightarrow4\left(2x+y\right)=11\left(3x-y\right)\)
\(\Leftrightarrow8x+4y=33x-11y\)
\(\Leftrightarrow15y=25x\)
\(\Leftrightarrow3y=5x\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{5}=k\)
\(\Rightarrow x=3k,y=5k\)
Thay vào Q ta có:
\(Q=\dfrac{2\cdot\left(3k\right)^2-3\cdot3k\cdot5k}{\left(3k\right)^2+3\cdot\left(5y\right)^2}\)
\(Q=\dfrac{18k^2-45k^2}{9k^2+75k^2}\)
\(Q=\dfrac{k^2\left(18-45\right)}{k^2\left(9+75\right)}\)
\(Q=\dfrac{-27}{84}=-\dfrac{9}{28}\)
27 tháng 7 2023
\(\dfrac{2x+y}{3x-y}=\dfrac{11}{4}\)
=>33x-11y=8x+4y
=>25x=15y
=>5x=3y
=>x/3=y/5=k
=>x=3k; y=5k
\(Q=\dfrac{2\cdot9k^2-3\cdot3k\cdot5k}{9k^2+3\cdot25k^2}=\dfrac{18-9\cdot5}{9+3\cdot25}=\dfrac{-9}{28}\)
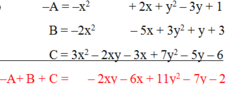
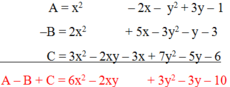
\(2x+3y=5\Rightarrow\left(\sqrt{2}.\sqrt{2}x+\sqrt{3}.\sqrt{3}y\right)^2=25\)từ đây bạn sẽ có
Áp dụng bất đẳng thức bunhiacopxki ta có:
\(25=\left(\sqrt{2}.\sqrt{2}x+\sqrt{3}.\sqrt{3}y\right)^2\le\left(2+3\right)\left(2x^2+3y^2\right)\)
hay
\(25\le5.\left(2x^2+3y^2\right)\Rightarrow2x^2+3y^2\ge5\)
vậy, min F = 5 <=> x = y = 1