xác định a để biểu thức sau nguyên:\(\)
\(\left[\dfrac{a^2-2a+4}{a-2}:\left(a^3+8\right)+\dfrac{a-2}{a^3+8}.\dfrac{a^2-2a+4}{a^2-4}\right]\left(a^2-4\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
27 tháng 5 2022
Đúng(1)
Những câu hỏi liên quan
2 tháng 7 2021
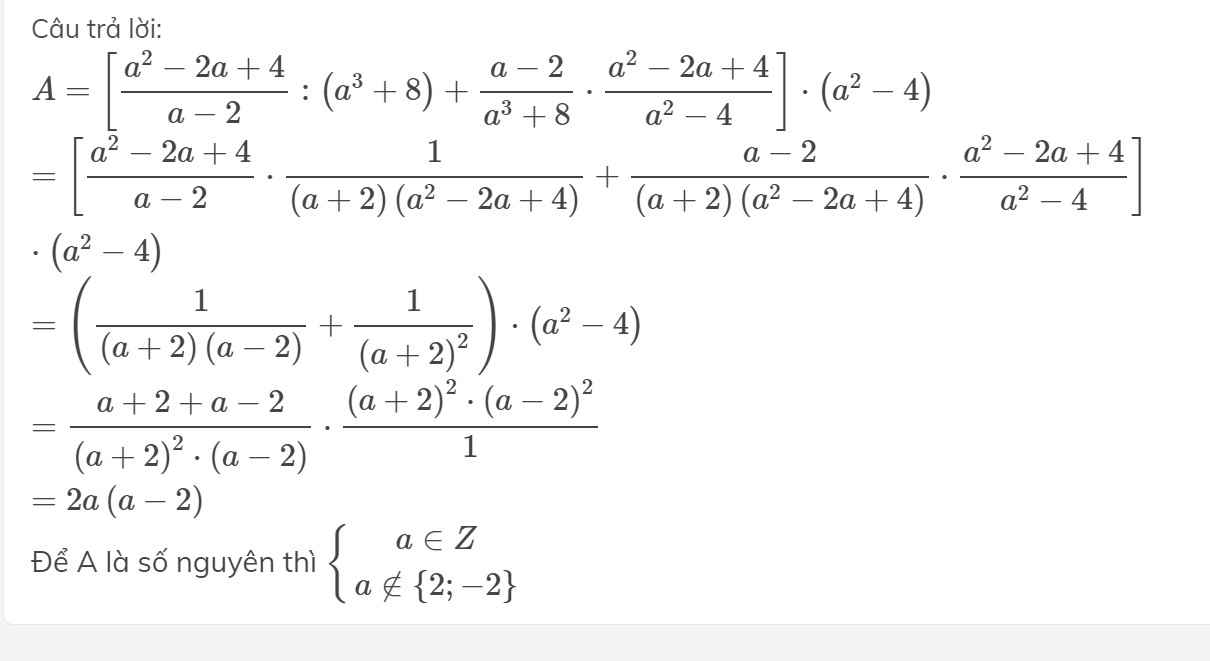
a) Ta có: \(A=\dfrac{a^2-1}{3}\cdot\sqrt{\dfrac{9}{\left(1-a\right)^2}}\)
\(=\dfrac{\left(a+1\right)\cdot\left(a-1\right)}{3}\cdot\dfrac{3}{\left|1-a\right|}\)
\(=\dfrac{\left(a+1\right)\left(a-1\right)}{1-a}\)
=-a-1
b) Ta có: \(B=\sqrt{\left(3a-5\right)^2}-2a+4\)
\(=\left|3a-5\right|-2a+4\)
\(=5-3a-2a+4\)
=9-5a
c) Ta có: \(C=4a-3-\sqrt{\left(2a-1\right)^2}\)
\(=4a-3-\left|2a-1\right|\)
\(=4a-3-2a+1\)
\(=2a-2\)
d) Ta có: \(D=\dfrac{a-2}{4}\cdot\sqrt{\dfrac{16a^4}{\left(a-2\right)^2}}\)
\(=\dfrac{a-2}{4}\cdot\dfrac{4a^2}{\left|a-2\right|}\)
\(=\dfrac{a^2\left(a-2\right)}{-\left(a-2\right)}\)
\(=-a^2\)
6 tháng 7 2021
1) Để biểu thức có nghĩa thì \(a^2+2a-3\ge0\)
\(\Leftrightarrow\left(a+3\right)\left(a-1\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-1\ge0\\a+3\le0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a\ge1\\a\le-3\end{matrix}\right.\)
2) Để biểu thức có nghĩa thì \(\left\{{}\begin{matrix}a-1\ge0\\a\ne0\end{matrix}\right.\Leftrightarrow a\ge1\)
3) Để biểu thức có nghĩa thì \(a>0\)
4) Để biểu thức có nghĩa thì \(\left\{{}\begin{matrix}a\ne-\dfrac{1}{2}\\\left[{}\begin{matrix}a-1\ge0\\2a+1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ne-\dfrac{1}{2}\\\left[{}\begin{matrix}a\ge1\\a< -\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a\ge1\\a< -\dfrac{1}{2}\end{matrix}\right.\)
AT
6 tháng 7 2021
1) Để biểu thức có nghĩa \(\Rightarrow a^2+2a-3\ge0\Rightarrow\left(a-1\right)\left(a+3\right)\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a-1\ge0\\a+3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}a-1\le0\\a+3\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a\ge1\\a\le-3\end{matrix}\right.\)
2) Để biểu thức có nghĩa \(\Rightarrow\dfrac{\left(a-1\right)^3}{a^2}\ge0\Rightarrow\left\{{}\begin{matrix}\left(a-1\right)^3\ge0\\a\ne0\end{matrix}\right.\Rightarrow a\ge1\)
3) Để biểu thức có nghĩa \(\Rightarrow\dfrac{a^2+1}{2a}\ge0\Rightarrow2a>0\Rightarrow a>0\)
4) Để biểu thức có nghĩa \(\Rightarrow\dfrac{a-1}{2a+1}\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a-1\ge0\\2a+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}a-1\le0\\2a+1< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a\ge1\\a< -\dfrac{1}{2}\end{matrix}\right.\)
28 tháng 6 2021
`M=sqrt{(3a-1)^2}+2a-3`
`=|3a-1|+2a-3`
`=3a-1+2a-3(do \ a>=1/3)`
`=5a-4`
`N=sqrt{(4-a)^2}-a+5`
`=|4-a|-a+5`
`=a-4-a+5(do \ a>4)`
`=1`
`I=sqrt{(3-2a)^2}+2-7`
`=|3-2a|-5`
`=3-2a-5(do \ a<3/2)`
`=-2-2a`
`K=(a^2-9)/4*sqrt{4/(a-2)^2}`
`=(a^2-9)/4*|2/(a-2)|`
`=(a^2-9)/(2|a-2|)`
Nếu `3>a>2=>|a-2|=a-2`
`=>K=(a^2-9)/(2(a-2))`
Nếu `a<2=>|a-2|=2-a`
`=>K=(a^2-9)/(2(2-a))`
28 tháng 6 2021
\(M=\left|3a-1\right|+2a-3\)
Mà \(a-\dfrac{1}{3}\ge0\)
\(\Rightarrow M=3a-1+2a-3=5a-4\)
\(N=\left|4-a\right|-a+5\)
Mà \(4-a< 0\)
\(\Rightarrow N=a-4-a+5=1\)
\(I=\left|3-2a\right|-5\)
Mà \(a-\dfrac{3}{2}< 0\)
\(\Rightarrow I=3-2a-5=-2a-2\)
K, Ta có : \(a-3< 0\)
\(\Rightarrow K=\dfrac{2\left(a^2-9\right)}{4\left|a-2\right|}=\dfrac{\left(a-3\right)\left(a+3\right)}{\left|2a-4\right|}\)
26 tháng 11 2021
\(B=\left(\dfrac{a-b}{a^2+ab}-\dfrac{a}{b^2+ab}\right):\left(\dfrac{b^3}{a^3-ab^2}+\dfrac{1}{a+b}\right)\)
\(=\left(\dfrac{a-b}{a\left(a+b\right)}-\dfrac{a}{b\left(a+b\right)}\right):\left(\dfrac{b^3}{a\left(a-b\right)\left(a+b\right)}+\dfrac{1}{a+b}\right)\)
\(=\dfrac{b\left(a-b\right)-a^2}{ab\left(a+b\right)}:\dfrac{b^3+a\left(a-b\right)}{a\left(a-b\right)\left(a+b\right)}\)
\(=\dfrac{ab-b^2-a^2}{ab\left(a+b\right)}\cdot\dfrac{a\left(a-b\right)\left(a+b\right)}{a^2-ab+b^3}\)
\(=\dfrac{\left(a-b\right)\left(ab-b^2-a^2\right)}{b\left(a^2-ab+b^3\right)}\)
\(=\dfrac{-\left(a-b\right)\left(a^2-ab+b^2\right)}{b\left(a^2-ab+b^3\right)}\)
Đề lỗi rồi chứ mình ko rút gọn đc nữa
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
\(VT=\dfrac{3}{4}-\dfrac{1}{2}-\dfrac{1}{2}cos\left(2a-\dfrac{2\pi}{3}\right)+\dfrac{1}{2}cos\left(2a-\dfrac{\pi}{3}\right)+\dfrac{1}{2}cos\left(\dfrac{\pi}{3}\right)\)
\(=\dfrac{1}{2}+\dfrac{1}{2}\left[cos\left(2a-\dfrac{\pi}{3}\right)-cos\left(2a-\dfrac{2\pi}{3}\right)\right]\)
\(=\dfrac{1}{2}-sin\left(2a-\dfrac{\pi}{2}\right)sin\left(\dfrac{\pi}{6}\right)\)
\(=\dfrac{1}{2}+\dfrac{1}{2}cos2a=\dfrac{1}{2}+\dfrac{1}{2}\left(2cos^2a-1\right)=cos^2a\)