Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ΔABC cân tại A có AM là đường trung tuyến
⇒ AM là tia phân giác của góc (BAC)
⇒ ∠ (BAM) = ∠ (MAC) (1)
Kéo dài MA cắt DE tai N, ta có:
∠ (BAM) = ∠ (DAN) (đối đỉnh) (2)
∠ (MAC) = ∠ (NAE) (đối đỉnh)(3)
Từ (1), (2) và (3) suy ra: ∠ (DAN) = ∠ (NAE)
∆ ADE cân tại A có AN là tia phân giác
⇒ AN là đường trung trực của DE
hay AM là đường trung trực của DE
Vậy D đối xứng với E qua AM.
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Bài làm
Gọi giao điểm của MA và ED là I
Xét tam giác cân ABC có:
=> \(\widehat{B}=\widehat{C}\)( hai góc ở đáy )
\(\Rightarrow\widehat{B}=\frac{180^0-\widehat{EAD}}{2}\) ( 1 )
Xét tam giác cân AED có: ( Vì EA = DA )
=> \(\widehat{E}=\widehat{D}\)
\(\Rightarrow\widehat{D}=\frac{180^0-\widehat{BAC}}{2}\)( 2 )
Mà \(\widehat{BAC}=\widehat{EAD}\)( Hai góc đối đỉnh )
Từ ( 1 ) và ( 2 ) => \(\widehat{B}=\widehat{D}\)
Mà hai góc này ở vị trí so le trong
=> ED // AM ( 3 )
Ta có: Tam giác ABC là tam giác cân.
Và M là trung điểm của BC
=> AM là đường trung tuyến của tam giác ABC
=> AM cũng là đường cao
=> AM | BC ( 4 )
Từ ( 3 ) và ( 4 ) => AI | ED
=> AI cũng là đường cao của ED
Và tam giác AED là tam giác cân
=> MA cũng là đường trung tuyến của của ED
=> EI = ID
=> E đối xứng với cả D qua AI
hay E đối xứng với D qua AM ( đpcm )
# Học tốt #
Vì ∆ABC cân tại A
Mà AM là trung tuyến BC
=> AM là trung trực và phân giác ∆ABC
=> BAM = CAM
Gọi O là giao điểm AM và DE
Mà OAC = OAD ( đối đỉnh )
BAO = OAE ( đối đỉnh )
Mà BAO = CAO (cmt)
=> OAD = OAE
Hay AO là phân giác DAE(1)
Mà AD = AE
=> ∆ADE cân tại A(2)
Từ (1) và (2)
=> AO là trung trực ∆ADE
=> AO = OC
AO\(\perp\)DE
Hay D và E đối xứng qua AM
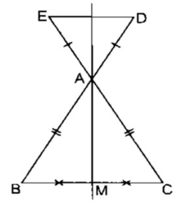
Câu 1:
Xét ΔEAB và ΔDAC có
AE=AD
\(\widehat{EAB}=\widehat{DAC}\)
AB=AC
Do đó: ΔEAB=ΔDAC
Suy ra: EB=DC và \(\widehat{EBA}=\widehat{DCA}\)
=>\(\widehat{EBC}=\widehat{DCB}\)
Xét ΔEBM và ΔDCM có
EB=DC
\(\widehat{EBM}=\widehat{DCM}\)
MB=MC
Do đó: ΔEBM=ΔDCM
Suy ra: ME=MD
mà AE=AD
nên AM là đường trung trực của ED
=>E đối xứng với D qua AM