Tìm x biết \(x+1=15-\sqrt{36}x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 6 2019
Ta có : \(x+3-4\sqrt{x-1}=\left(\sqrt{x-1}-2\right)^2\)và \(x+15-8\sqrt{x-1}=\left(\sqrt{x-1}-4\right)^2\)
Suy ra: B=\(\sqrt{x-1}-2+\sqrt{x-1}-4=2\sqrt{x-1}-6\)
Ta lại có : \(x-1\ge0\)=>\(B\ge-6\)dấu ''='' xảy ra khi: x-1=0 <=>x=1
Vậy minB=-6 khi x=1
TH
4
LT
6 tháng 3 2020
suy ra3.(5x-1) - 4.(5x-1) + 6(5x-1) =15
suy ra 5.(5x-1) = 15
suy ra 5x-1=3
suy ra x=4/5
6 tháng 3 2020
\(\Leftrightarrow3\left(5x-1\right)-4\left(5x-1\right)+6\left(5x-1\right)=15\)
\(\Leftrightarrow\left(3-4+6\right)\left(5x-1\right)=15\)
\(\Leftrightarrow5\left(5x-1\right)=15\)
\(\Leftrightarrow5x-1=\frac{15}{5}=3\)
\(\Leftrightarrow5x=3+1=4\)
\(\Leftrightarrow x=\frac{4}{5}\)
Vậy \(x=\frac{4}{5}\)
29 tháng 4 2021
a, \(\sqrt{\left(2x-1\right)^2}=3\Leftrightarrow\left|2x-1\right|=3\)
Với \(x\ge\frac{1}{2}\)pt có dạng : \(2x-1=3\Leftrightarrow x=2\)( tm )
Với \(x< \frac{1}{2}\)pt có dạng : \(-2x+1=3\Leftrightarrow x=-1\)( tm )
Vậy tập nghiệm của pt là S = { -1 ; 2 }
b, \(\frac{5}{3}\sqrt{15x}-\sqrt{15x}-2=\frac{1}{3}\sqrt{15x}\)ĐK : \(x\ge0\)
\(\Leftrightarrow\frac{2}{3}\sqrt{15x}-2=\frac{1}{3}\sqrt{15x}\Leftrightarrow\frac{1}{3}\sqrt{15x}=2\)
\(\Leftrightarrow\sqrt{15x}=6\)bình phương 2 vế : \(\Leftrightarrow15x=36\Leftrightarrow x=\frac{36}{15}=\frac{12}{5}\)( tm )
Vậy tập nghiệm của pt là S = { 12/5 }
17 tháng 5 2021
)
√
(
2
x
−
1
)
2
=
3
⇒
|
2
x
−
1
|
=
3
⇔
2
x
−
1
=
±
3
+) TH1:
2
x
−
1
=
3
⇒
2
x
=
4
⇒
x
=
2
+) TH2:
2
x
−
1
=
−
3
⇒
2
x
=
−
2
⇒
x
=
−
1
Vậy
x
=
−
1
;
x
=
2
.
b) Điều kiện:
x
≥
0
5
3
√
15
x
−
√
15
x
−
2
=
1
3
√
15
x
⇔
5
3
√
15
x
−
√
15
x
−
1
3
√
15
x
=
2
⇔
(
5
3
−
1
−
1
3
)
√
15
x
=
2
⇔
1
3
√
15
x
=
2
⇔
√
15
x
=
6
⇔
15
x
=
36
⇔
x
=
12
5
Vậy
x
=
12
5
.
PT
1
CM
22 tháng 8 2019
a) 2x + 36 : 12 = 53
2x + 3 = 53
2x = 53 – 3
2x = 50
x = 25
b) |x + 7| = |- 15|
|x + 7| = 15
x + 7 = 15 hoặc x + 7 = - 15
x = 15 – 7 hoặc x = -15 – 7
x = 8 hoặc x = - 22
c) 19 – | x – 1 | = 4
| x – 1 | = 15
x – 1 = 15 hoặc x – 1 = -15
x = 15 + 1 hoặc x = -15 + 1
x = 16 hoặc x = - 14
PT
1
PC
1
YN
4
12 tháng 9 2020
Ta có: \(5\sqrt{x-1}-\sqrt{36x-36}+\sqrt{9x-9}=\sqrt{8x+12}\) \(\left(ĐK:x\ge1\right)\)
\(\Leftrightarrow5\sqrt{x-1}-6\sqrt{x-1}+3\sqrt{x-1}=\sqrt{8x+12}\)
\(\Leftrightarrow2\sqrt{x-1}=\sqrt{8x+12}\)
\(\Leftrightarrow\left(2\sqrt{x-1}\right)^2=\left(\sqrt{8x+12}\right)^2\)
\(\Leftrightarrow4.\left(x-1\right)=8x+12\)
\(\Leftrightarrow4x-4=8x+12\)
\(\Leftrightarrow-4x=16\)
\(\Leftrightarrow x=-4\left(L\right)\)
Vậy \(S=\varnothing\)
12 tháng 9 2020
\(5\sqrt{x-1}-\sqrt{36\left(x-1\right)}+\sqrt{9\left(x-1\right)}=\sqrt{4\left(2x+3\right)}\)
\(5\sqrt{x-1}-6\sqrt{x-1}+3\sqrt{x-1}=2\sqrt{2x+3}\)
\(2\sqrt{x-1}=2\sqrt{2x+3}\)
\(\sqrt{x-1}=\sqrt{2x+3}\)
\(\hept{\begin{cases}2x+3\ge0\\x-1=2x-3\end{cases}}\)
\(\hept{\begin{cases}2x\ge-3\\x-2x=-3+1\end{cases}}\)
\(\hept{\begin{cases}x\ge-\frac{3}{2}\\-x=-2\end{cases}}\)
\(\hept{\begin{cases}x\ge-\frac{3}{2}\\x=2\end{cases}}\)
\(\Rightarrow x=2\)
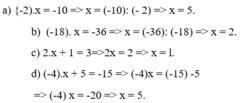
x+1=15-\(\sqrt{36}\)x
<=>x+1=15-6x
<=>x+6x=15-1
<=>7x=14
<=>x=2