Cho Δ ABC. Trung tuyến BD, CE. Gọi M, N lần lượt là trung điểm của BE, CD. Gọi I, K lần lượt là giao điểm của MN với BD, CE. Chứng minh rằng : MI = IK = KN
Các bạn giúp mình nhé lát nữa mình phải nộp rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DV
Đời về cơ bản là buồn... cười!!!
19 tháng 8 2017
Đúng(0)
Những câu hỏi liên quan
21 tháng 8 2018
bn học hình thang rồi chứ
a,Xét tam giác ABC có: E là tđ của AB
D là tđ của AC
=> ED là đường TB của tam giác ABC
=> \(ED=\frac{1}{2}BC\left(1\right)\),ED//BC
Xét hình thang EDCB(ED//BC) có M là tđ của BE, N là tđ của CD
=> MN là đường TB của hình thang EDCB
=> MN//BC. Mà I,K nằm trên MN
=> MK//BC, NI//BC
Xét tam giác ECB có: M là tđ của EB, MK//BC
=> K là tđ của CE
C/m tương tự ta có
I là tđ của BD
Xét tam giác ECB có M là tđ của BE, K là tđ của CE
=> MK là đường TB của tam giác EBC
=>\(MK=\frac{1}{2}BC\left(2\right)\)
C/m Tương tự ta có
\(IN=\frac{1}{2}BC\left(3\right)\)
Từ (1),(2),(3)=> đpcm
27 tháng 8 2018
b, theo a ta có :M là tđ của BE
N là tđ của CD
Dễ dàng c/m đc MI là đg TB của tam giác BED(M là tđ, I là tđ)
=> MI// và =\(\frac{1}{2}ED\left(1\right)\)
C/m T2 ta có:
\(KN=\frac{1}{2}ED\left(2\right)\)
(Ta áp dụng t/c:Trong HT có 2 cạnh bên ko //, đoạn thẳng nối tđ 2 đg chéo thì // với đáy và = \(\frac{1}{2}\) hiệu 2 đáy)
Ta có: I là tđ của BD,K là tđ của CE
=>\(IK=\frac{BC-ED}{2}=\frac{2ED-ED}{2}=\frac{1}{2}ED\left(3\right)\)
Từ (1),(2),(3)=> đpcm
các bn thấy đúng tk cho mk nha
3 tháng 7 2017
sao N đã là trung điểm CE mà MN còn cắt CE tại K nữa?
HA
4 tháng 7 2017
Gọi M và N theo thứ tự là trung điểm của BE và CD nhé , mình viết nhầm thành CE
CM
13 tháng 1 2017
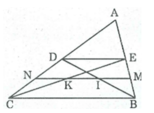
Trong ∆ ABC ta có: E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ ED // BC và ED = 1/2 BC
(tính chất đường trung bình của tam giác)
+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE
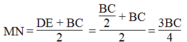
(tính chất đường trung bình hình thang)
Trong ∆ BED, ta có: M là trung điểm BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
Trong ∆ CED ta có: N là trung điểm CD
NK // DE
Suy ra: NK là đường trung bình của ∆ CED
⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC
⇒ MI = IK = KN = 1/4 BC