mọi ngừoi giúp em
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Ta có
- \(Cl=35,5đvC\)
- Đơn chất \(Cl=71đvC\)
- Số nguyên tử Cl trong 1 phân tử Cl \(=\dfrac{71}{35,5}=2\)
Vậy: Số nguyên tử Cl trong 1 phân tử Cl là 2

a,\(3xy+6x^2=3x\left(y+2x\right)\)
b,\(-4xy^2+8x^2y=-4xy\left(y-2x\right)\)
c,\(4\left(x+y\right)+x^2+xy=4\left(x+y\right)+x\left(x+y\right)\)\(=\left(4+x\right)\left(x+y\right)\)
d,\(4x^2-9y^2=\left(2x\right)^2-\left(3y\right)^2=\left(2x-3y\right)\left(2x+3y\right)\)
e,\(25x^2-\dfrac{1}{4}=\left(5x\right)^2-\left(\dfrac{1}{2}\right)^2=\left(5x-\dfrac{1}{2}\right)\left(5x+\dfrac{1}{2}\right)\)

Câu 14:
\(R_{tđ}=R_1+R_2+R_3=12+15+13=40\left(\Omega\right)\)
\(I=I_1=I_2=\dfrac{U}{R}=\dfrac{12}{40}=0,3\left(A\right)\)
Câu 15:
\(R=\rho\dfrac{l}{S}=0,40.10^{-6}.\dfrac{10}{0,1.10^{-6}}=40\left(\Omega\right)\)
\(I=\dfrac{U}{R}=\dfrac{12}{40}=0,3\left(A\right)\)

a: Xét ΔABC có \(\widehat{ABC}=\widehat{ACB}\)
nên ΔABC cân tại A
hay AB=AC


`@` `\text {Ans}`
`\downarrow`
\(1793\cdot\left(x\div1792\right)=0\)
`\Rightarrow x \div 1792 = 0 \div 1793`
`\Rightarrow x \div 1792 = 0`
`\Rightarrow x = 0. 1792`
`\Rightarrow x = 0`
Vậy, `x = 0.`
\(1793.\left(x:1792\right)=0\)
\(=>x:1792=0:1793\)
\(=>x:1792=0\)
\(=>x=0.1792\)
\(=>x=0\)

uk bn Long Sơn nói đúng đấy hôm qua vừa có đề cương giữa kì 2 nhìn là biết


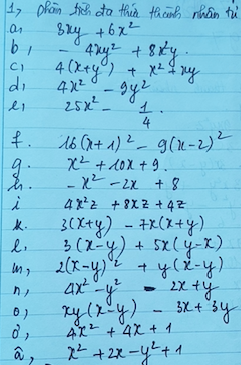

 nãy em chọn lộn môn hoá em xin lỗi ạ :> mọi ngừoi giúp em với em cần gấp ạ
nãy em chọn lộn môn hoá em xin lỗi ạ :> mọi ngừoi giúp em với em cần gấp ạ
a, Với \(x\ge0;x\ne25\)
\(A=\frac{\sqrt{x}}{\sqrt{x}-5}-\frac{10\sqrt{x}}{x-25}-\frac{5}{\sqrt{x}+5}\)
\(=\frac{x+5\sqrt{x}-10\sqrt{x}-5\sqrt{x}+25}{x-25}=\frac{x-10\sqrt{x}+25}{x-25}=\frac{\sqrt{x}-5}{\sqrt{x}+5}\)
b, Thay x = 121 => \(\sqrt{x}=11\)ta được : \(\frac{11-5}{11+5}=\frac{6}{16}=\frac{3}{8}\)
c, Ta có : \(A=\left|\frac{\sqrt{x}-5}{\sqrt{x}+5}\right|=\frac{1}{4}\)
TH1 : \(\frac{\sqrt{x}-5}{\sqrt{x}+5}=\frac{1}{4}\Rightarrow4\sqrt{x}-20=\sqrt{x}+5\Leftrightarrow3\sqrt{x}=25\Leftrightarrow\sqrt{x}=\frac{25}{3}\Leftrightarrow x=\frac{625}{9}\)
TH2 : \(\frac{\sqrt{x}-5}{\sqrt{x}+5}=-\frac{1}{4}\Rightarrow4\sqrt{x}-20=-\sqrt{x}-5\Leftrightarrow5\sqrt{x}=15\Leftrightarrow x=9\)