ch phương trình ax2 +bx +c=0 biết a#0 và 5a +4b+6c=0 chứng minh rằng phương trình đã cho có hai nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

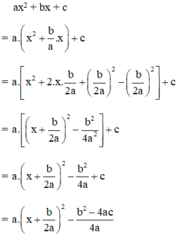
Ta có: a > 0 (gt), 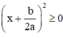 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 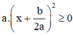
Phương trình ax2 + bx + c = 0 vô nghiệm nên
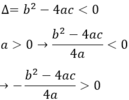
Vậy
a
x
2
+
b
x
+
c
= 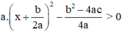 với mọi x.
với mọi x.

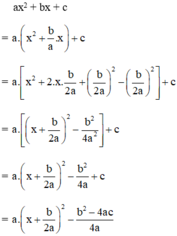
Ta có: a > 0 (gt), 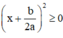 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 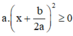
Phương trình ax2 + bx + c = 0 vô nghiệm nên
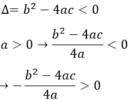
Vậy ax2 + bx + c = 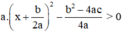 với mọi x.
với mọi x.

Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x

Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình
có nghiệm kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình
có hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: C

Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình có nghiệm
kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình có
hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: A

Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình
có nghiệm kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình
có hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: D

Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình
có nghiệm kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình
có hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: C
Lời giải:
PT đã cho có hai nghiệm khi mà \(\Delta=b^2-4ac>0\)
Theo điều kiện đề bài ta có:
\(\Delta=b^2-4ac=\left (\frac{-6c-5a}{4}\right)^2-4ac=\frac{(5a+6c)^2-64ac}{16}\)
\(\Leftrightarrow \Delta=\frac{25a^2+36c^2-4ac}{16}=\frac{24a^2+(a-2c)^2+32c^2}{16}\)
Vì \(a\neq 0\Rightarrow 24a^2+(a-c)^2+32c^2>0\Rightarrow \Delta>0\)
Do đó PT trên có hai nghiệm phân biệt.
\(f\left(x\right)=\text{ax}^2+bx+c\)
Nếu a=0 thì ta có: \(4b+6c=0\) hay \(c=\dfrac{-2}{3}b\). Phương trình có dạng
\(bx-\dfrac{2}{3}b=0\Leftrightarrow x=\dfrac{2}{3}\) là 1 nghiệm
Xét \(a\ne0\). Khi đó
\(5a+4b+6c=0\Leftrightarrow\left(4a+2b+c\right)+\left(a+2b+4c\right)+c=0\)
\(f\left(2\right)+\dfrac{1}{4}f\left(\dfrac{1}{2}\right)+f\left(0\right)=0\)
\(\Leftrightarrow\text{af}\left(2\right)+\dfrac{1}{4}\text{af}\left(\dfrac{1}{2}\right)+\text{af}\left(0\right)=0\)
=> Tồn tại ít nhất 1 số hạng âm hoặc bằng 0, theo định lý đảo suy ra phương trình có nghiệm