Bài 1: Phân tích đa thức thành nhân tử:
a, ( x2 + x )2 + 4( x2 + x ) - 12
b, ( x + 1)( x+ 2)( x + 3)( x + 4) - 24
Bài 2: Cmr với n lẻ thì:
a, n2 + 4n + 3 chia hết cho 8.
b, n3 + 3n2 - n - 3 chia hết cho 48.
c, n12 - n8 - n4 + 1 chia hết cho 512.
Help me!!! Các pạn ơi, bài 1 mk không biết chắc là dấu trừ hay dấu bằng trước số 12 hay là 24, các p ktra lại rùm mk đc k!!!

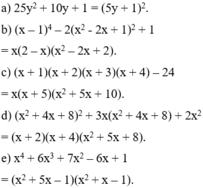
a) \(\left(x^2+x\right)^2+4\left(x^2+x\right)-12\)
\(=x^4+2x^3+x^2+4x^2+4x-12\)
\(=x^4-x^3+2x^3-2x^2+x^3-x^2+2x^2-2x+6x^2-6x+12x-12\)
\(=x^3\left(x-1\right)+2x^2\left(x-1\right)+x^2\left(x-1\right)+2x\left(x-1\right)+6x\left(x-1\right)+12\left(x-1\right)\)
\(=\left(x^3+ 2x^2+x^2+2x+6x+12\right)\left(x-1\right)\)
\(=\left[x^2\left(x+2\right)+x\left(x+2\right)+6\left(x+2\right)\right]\left(x-1\right)\)
\(=\left(x^2+x+6\right)\left(x-1\right)\left(x+2\right)\)
b) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left(x^2+x+2x+2\right)\left(x^2+3x+4x+12\right)-24\)
\(=x^4+x^3+2x^3+2x^2+3x^3+3x^2+6x^2+6x+4x^3+4x^2+8x^2+8x+12x^2+12x+24x+24\)
\(=x^4+5x^3+5x^3+5x^2+10x^2+50x\)
\(=x^2\left(x^2+5x\right)+5x\left(x^2+5x\right)+10\left(x^2+5x\right)\)
\(=\left(x^2+5x+10\right)\left(x^2+5x\right)\).
Bài 1:
a, \(\left(x^2+x\right)^2+4\left(x^2+x\right)-12\)
\(=\left(x^2+x\right)^2+2.2\left(x^2+x\right)+4-16\)
=\(\left(x^2+x+2\right)^2-4^2\)
=\(\left(x^2+x-2\right)\left(x^2+x+6\right)\)
b,\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)
=\(\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)-24\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\) (1)
Đặt \(x^2+5x+5=a\) thay vào (1) đc:
(1) = \(\left(a-1\right)\left(a+1\right)-24=a^2-25\)
\(=\left(a-5\right)\left(a+5\right)\)\(=\left(x^2+5x\right)\left(x^2+5x+10\right)\)
Bài 2:
\(a,n^2+4n+3=n^2+n+3n+3\)
\(=n(n+1)+3\left(n+1\right)=\left(n+1\right)\left(n+3\right)\)Đặt \(n=2k+1\)
\(\Rightarrow\left(n+1\right)\left(n+3\right)=\left(2k+2\right)\left(2k+4\right)\)
Mà tích của 2 số nguyên chẵn liên tiếp thì chia hết chia hết cho 8
\(\Rightarrowđpcm\)
b,\(n^3+3n^2-n-3=n^2\left(n+3\right)-\left(n+3\right)\)\(=\left(n+3\right)\left(n^2-1\right)\)\(=\left(n+3\right)\left(n+1\right)\left(n-1\right)\)
Mà 48 = 24.3
Đặt \(n=2k+1\) thì
(1) = \(\left(2k+4\right)\left(2k+2\right)2k\)
Tích của 3 số nguyên chẵn liên tiếp thì chia hết cho 16 (I)
Tích của số chẵn liên tiếp thì có một số là bội của 3 (II)
(I);(II)\(\Rightarrow\)đpcm
c,512 = 29
\(n^{12}-n^8-n^4+1=n^8\left(n^4-1\right)-\left(n^4-1\right)\)\(=(n^4-1)\left(n^8-1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\left(n^4+1\right)\)Đặt \(n=2k+1\) thay vào đc:
\(2k\left(2k+2\right)\left(4k^2+4k+2\right)2k\left(2k+2\right)\).
\(\left(4k^2+4k+2\right)\left(16k^4+32k^3+24k^2+8k+2\right)\)Bạn tự chứng minh tiếp nhá!!