Cho đường tròn tâm O đường kính AB=10cm. Dây CD cắt AB tại I và tạo với đường kính đó là góc 45'. Biết ID= 7 IC. Tính IC, ID, IO.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 7 2017
Kẻ \(OH⊥DC\Rightarrow HC=HD\) (theo tính chất của dây cung )
Có \(AB=10\Rightarrow OC=OD=R=5\left(cm\right)\)
Mà \(ID=7IC\Rightarrow CD=IC+ID=8IC\Rightarrow HC=HD=4IC\)
Theo giả thiết ta có \(\widehat{HIO}=45^0\Rightarrow\Delta IHO\)vuông cân tại H \(\Rightarrow HI=HO=HC-IC=3IC\)
Xét tam giác AHO có \(OH^2=5^2-HC^2\Rightarrow9IC^2=25-16IC^2\Rightarrow IC^2=1\Rightarrow IC=1\left(cm\right)\)
\(\Rightarrow ID=7IC=7\left(cm\right)\)
\(IO=\sqrt{IH^2+HO^2}=\sqrt{9+9}=3\sqrt{2}\left(cm\right)\)
Vậy \(IC=1cm;ID=7cm;IO=3\sqrt{2}cm\)
31 tháng 12 2023
Câu 1:
Gọi giao điểm của OC với AB là H
Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H
=>OH là khoảng cách từ O xuống dây AB
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2=8(cm)
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=10^2-8^2=36\)
=>\(OH=\sqrt{36}=6\left(cm\right)\)
Câu 2:
a: Xét (O) có
AB là đường kính
BC là dây
Do đó: AB>BC
b: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
c: Xét ΔACB có
O là trung điểm của AB
OM//CB
Do đó: M là trung điểm của AC
CM
28 tháng 5 2018
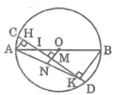
Kẻ OM ⊥ CD cắt AD tại N
Ta có: MC = MD (đường kính dây cung)
Hay MH + CH = MK + KD (1)
Ta có: OM // BK (cùng vuông góc với CD)
Hay: MN // BK
Mà: OA = OB (= R)
Suy ra: NA = NK (tính chất đường trung bình của tam giác)
Lại có: OM // AH (cùng vuông góc với CD)
Hay: MN // AH
Mà: NA = NK (chứng minh trên)
Suy ra: MH = MK (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: CH = DK
HH
20 tháng 1 2021
Ta có : \(AH\perp CD\left(gt\right)\)
\(BK\perp CD\left(gt\right)\)
=> AH // BK
=> Tứ giác ABKH là hình thang có đáy AH và BK
Theo ( gt ) : OA = OB mà \(OM\perp CD\)( theo cách dựng )
=> OM // AC / BK
=> MK = MH (1)
Mặt khác : \(OM\perp CD\Rightarrow MC=MD\left(2\right)\)
Từ (1) và (2) => MH - MC = MK - MD
=> CH = DK
Vậy CH = DK