Một đồng hồ có kim giây dài gấp 1,5 lần kim phút của nó. Hãy so sánh tốc độ góc, tốc độ dài và gia tốc hướng tâm của hai đầu kim.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
15 tháng 10 2021
Ta có công thức tính tốc độ dài của kim giờ và kim phút như sau:
\(v_p=\omega r_p=\dfrac{2\pi r_p}{T_p}vav_g=\omega r_g=\dfrac{2\pi r_g}{T_g}\)
\(\Rightarrow\dfrac{v_p}{v_g}=\dfrac{r_p}{r_g}.\dfrac{T_g}{T_p}\)
Thay: \(r_p=1,5r_g;T_p=3600s;T_g=43200s\) vào công thức trên, ta có:
\(\dfrac{v_p}{v_g}=\dfrac{1,5r_g}{r_g}.\dfrac{43200}{3600}18lan\)
30 tháng 10 2021
Kim giây quay 1 vòng hết 60s\(\Rightarrow T=60\)s
Tốc độ góc của kim giây:
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{60}=\dfrac{1}{30}\pi\)(rad/s)
Tốc độ dài của kim giây: \(v=r\cdot\omega=0,1\cdot\dfrac{1}{30}\pi=\dfrac{1}{300}\pi\)(m/s)
Gia tốc hướng tâm:
\(a_{ht}=r\cdot\omega^2=0,1\cdot\left(\dfrac{1}{30}\pi\right)^2\approx1,1\cdot10^{-3}\)(m/s2)
VT
2 tháng 3 2019
Tốc độ dài của đầu kim phút và kim giờ được tính theo công thức:
Từ đó suy ra
Thay r 1 = 1,5 r 2 ; T 1 = 3600 s; T 2 = 43200 s vào công thức trên ta tìm được
VT
19 tháng 6 2019
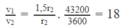
Chọn đáp án A
Điểm đầu các kim của đồng hồ chuyển động tròn đều
Gọi ω 1 , ω 2 lần lượt là tốc độ góc của kim phút và kim giờ. Chiều dài của kim phút và kim giờ tương ứng là R 1 , R 2 ta có:
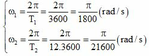
Theo đề bài R 1 = 2 R 2
Tốc độ dài ở điểm đầu kim phút và kim giờ lần lượt là
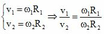
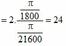
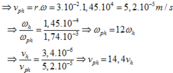
\(\dfrac{\omega_1}{\omega_2}\)=\(\dfrac{T_2}{T_1}\)=60
\(\dfrac{v_1}{v_2}\)=\(\dfrac{\omega_1R_1}{\omega_2R_2}\)=60.1,5=90
\(\dfrac{a_{ht1}}{a_{ht2}}\)=\(\dfrac{\omega_1^2R_1}{\omega_2^2R_2}\)=602.1,5=5400