Cho hai đường thẳng AB và CD cắt nhau tại M. Biết rằng \(\widehat{BMC}=3\widehat{CMA}\). Tính số đo các góc.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 7 2021
Có \(\widehat{CMA}+\widehat{CMB}=180^0\) (Hai góc kề bù)
\(\Leftrightarrow5\widehat{CMA}+\widehat{CMA}=180^0\Leftrightarrow\widehat{CMA}=30^0\)
\(\Rightarrow\widehat{BMC}=5.30^0=150^0\)
Có \(\widehat{CMA}+\widehat{AMD}=180^0\)
\(\Leftrightarrow\widehat{AMD}=180^0-30^0=150^0\)
Có \(\widehat{DMB}=\widehat{AMC}=150^0\) (Hai góc đối đỉnh)
Vậy...
N
6 tháng 9 2019
Ta có: \(\widehat{AMC}+\widehat{AMD}=180^o\)(2 góc kề bù) (1)
Mà \(\widehat{AMC}=2\widehat{AMD}\)(Đề cho) (Ngoặc ''}'' 2 điều lại)
=> \(2\widehat{AMD}+\widehat{AMD}=180^o\)
=> \(\left(2+1\right)\widehat{AMD}=180^o\)
=> \(3\widehat{AMD}=180^o\)
=> \(\widehat{AMD}=180^o:3\)
=> \(\widehat{AMD}=60^o\)(2)
Từ (1) và (2) => \(\widehat{AMC}=180^o-60^o=120^o\)
Lại có: \(\widehat{AMC}=\widehat{BMD}\)(2 góc đối đỉnh) (Ngoặc ''}'' 2 điều lại)
=> \(\widehat{BMD}=120^o\)
Mặt khác: \(\widehat{AMD}=\widehat{BMC}\)(2 góc đối đỉnh)
Mà \(\widehat{AMD}=60^o\)(Theo (2)) (Ngoặc ''}'' 2 điều lại)
=> \(\widehat{BMC}=60^o\)
Vậy \(\widehat{AMC}=\widehat{BMD}=120^o\)
\(\widehat{AMD}=\widehat{BMC}=60^o\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
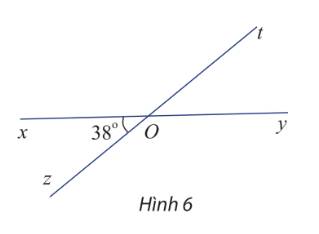
Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)
hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)
\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \)
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)
T
28 tháng 5 2019
#)Giải :
#)Giải :
Vì \(\widehat{AOC}\)và \(\widehat{BOD}\)là hai góc đối đỉnh \(\Rightarrow\widehat{AOC}=\widehat{BOD}\left(=70^o\right)\)
Vì \(\widehat{AOC}\)và \(\widehat{BOC}\)là hai góc kề bù
\(\Rightarrow\widehat{BOC}=180^o-\widehat{AOC}\)
\(=180^o-70^o\)
\(=110^o\)
\(\Rightarrow\widehat{BOC}=110^o\)
Vì \(\widehat{BOC}\)và \(\widehat{AOD}\)là hai góc đối đỉnh \(\Rightarrow\widehat{BOC}=\widehat{AOD}\left(=110^o\right)\)
#~Will~be~Pens~#
28 tháng 5 2019
Theo đề bài biết :
\(\widehat{AOC}\)- \(\widehat{BOC}\)= 70o
Ngoài ra còn biết :
\(\widehat{AOC}\)+ \(\widehat{BOC}\)= 180o ( kề bù )
\(\rightarrow\)\(\widehat{AOC}\)= ( 70o + 180o ) : 2 = 125o
\(\rightarrow\)\(\widehat{BOC}\)= 180o - 125o = 55o
Có \(\widehat{AOD}\)+ \(\widehat{AOC}\)= 180o ( kề bù )
\(\rightarrow\)\(\widehat{AOD}\)= 180o - \(\widehat{AOC}\)= 180o - 125o = 55o
Có \(\widehat{BOD}\)+ \(\widehat{BOC}\)= 180o ( kề bù )
\(\rightarrow\)\(\widehat{BOD}\)= 180o - \(\widehat{BOC}\)
180o - 55o = 125o
+) Ta có :
\(AMC+CMB=180^0\) (kề bù)
Mà \(BMC=3.CMA\)
\(\Leftrightarrow CMA+3CMA=180^0\)
\(\Leftrightarrow CMA.\left(1+3\right)=180^0\)
\(\Leftrightarrow CMA.4=180^0\)
\(\Leftrightarrow CMA=45^0\)
\(\Leftrightarrow BMC=135^0\)
+) Ta có :
\(AMC=BMD\) (đối đỉnh)
Mà \(AMC=45^0\)
\(\Leftrightarrow BMD=45^0\)
+) Ta có :
\(BMC=AMD\) (đối đỉnh)
Mà \(BMC=135^0\)
\(\Leftrightarrow AMD=135^0\)
BMC = 3 CMA, hình vẽ sai