Tìm tập hợp các điểm M có tọa độ như sau với mọi số thực m :
a, M (m ; -1) b, M (2 ; m)
c, M ( m ; m ) d, M (m ; -m)
Help me
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2023
a: Gọi (d): y=ax+b là tập hợp các điểm M cần tìm
Thay x=m và y=-1 vào (d), ta được;
ma+b=-1
=>ma=-1-b
=>m=(-b-1)/a
b: Thay x=2 và y=m vào (d), ta được:
2a+b=m
=>m=2a+b
c: Thay x=m và y=m vào (d), ta được:
ma+b=m
=>m(a-1)=m
=>m=m/(a-1)
=>M nằmtrên đường y=x
d: Vì M(m;-m) nên M nằm trên đường y=-x
21 tháng 8 2023
i:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/4 | 1/2 | 1 | 2 | 4 |
ii:
Hàm số liên tục và đồng biến trên R
\(\lim\limits_{x\rightarrow+\infty}2^x=+\infty;\lim\limits_{x\rightarrow-\infty}2^x=0\)
Tập giá trị: \((0;+\infty)\)
b:
bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 2 | 1 | 1/2 | 1/4 |
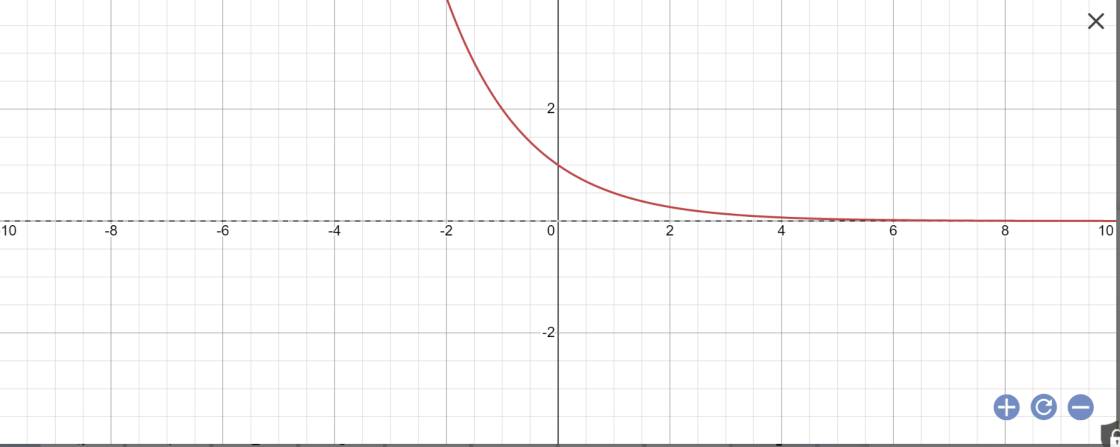
Hàm số liên tục và nghịch biến trên R
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{2}\right)^x=0;\lim\limits_{x\rightarrow-\infty}\left(\dfrac{1}{2}\right)^x=+\infty\)
Tập giá trị: (0;+\(\infty\))
21 tháng 8 2023
a:
i:
| x | 1/2 | 1 | 2 | 4 |
| y | -1 | 0 | 1 | 2 |
ii:
Hàm số liên tục và đồng biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_2x=+\infty;\lim\limits_{x\rightarrow0^+}log_2x=-\infty\)
Tập giá trị: R
b:
| x | 1/2 | 1 | 2 | 4 |
| y | 1 | 0 | -1 | -2 |
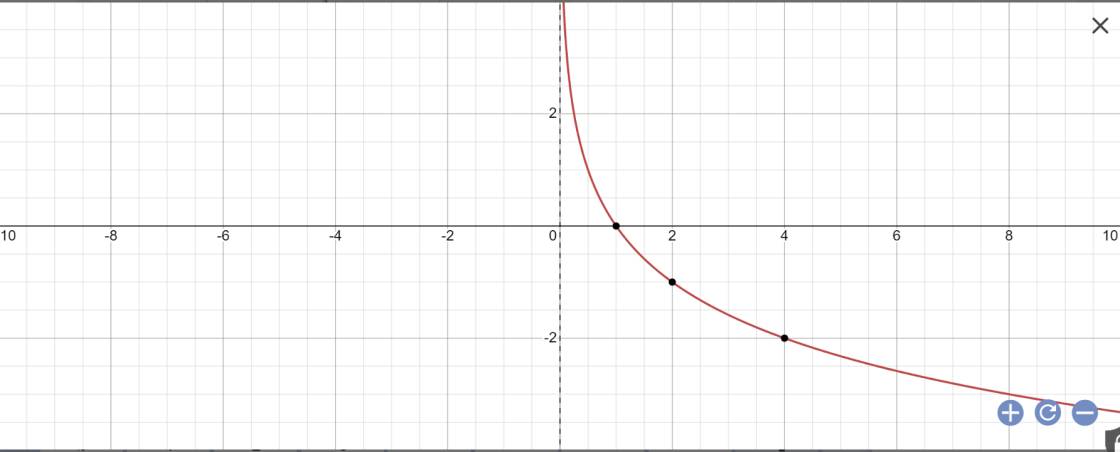
Hàm số liên tục và nghịch biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_{\dfrac{1}{2}}x=-\infty;\lim\limits_{x\rightarrow0^+}log_{\dfrac{1}{2}}x=+\infty\)
Tập giá trị: R
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Dựa vào hình vẽ ta thấy \(A\left( {1; - 3} \right)\)
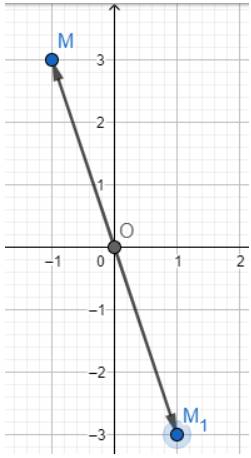
b) Dựa vào hình vẽ ta thấy \(B\left( { - 1; - 3} \right)\)
c) Dựa vào hình vẽ ta thấy \(C\left( {1;3} \right)\)
CM
27 tháng 3 2018
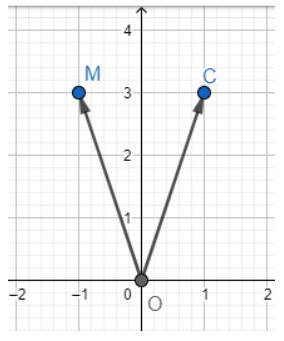
Đáp án A.
Gọi:
Phương trình mặt phẳng (P) có dạng:
Vì M là trực tâm của tam giác ABC nên
19 tháng 12 2022
a: vect OA=(3;-1)
vecto OB=(4;2)
Vì 3/4<>-1/2
nên O,A,B ko thẳng hàng
b: OABM là hình bình hành
nên vecto OA=vecto MB
=>4-x=3 và 2-y=-1
=>x=1 và y=3
c: Tọa độ I là:
x=(3+4)/2=3,5 và y=(-1+2)/2=0,5