Biện luận theo m số nghiệm của phương trình ( dựa vào đồ thị hàm số):
\(\left|-x^2+3x+2\right|=2m-1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: x + 1 3 = 3x + m (1)
⇔ x + 1 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = x + 1 3 − 3x – 4 (C’) và y = m – 4 ( d 1 )
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.

a:
b: \(\Delta=\left(-2m\right)^2-4\cdot1\cdot4=4m^2-16\)
Để phương trình có hai nghiệm phân biệt thì 4m^2-16>0
=>m>2 hoặc m<-2
Để phương trình có nghiệm duy nhất thì 4m^2-16=0
=>m=2 hoặc m=-2
Để phương trìh vô nghiệm thì 4m^2-16<0
=>-2<m<2

a)
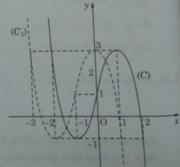
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
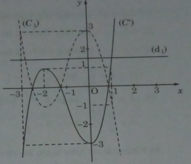
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
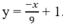
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 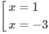
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.

Số nghiệm của phương trình x 3 + 3 x 2 + 1 = m 2 bằng số giao điểm của đồ thị (C) và đường thẳng y = m/2.
Từ đồ thị ta có:
+ Đường thẳng cắt đồ thị tại 1 điểm khi và chỉ khi :
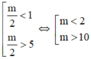
⇒ phương trình có 1 nghiệm.
+ Để đường thẳng cắt đồ thị tại 2 điểm phân biệt khi và chỉ khi :
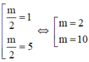
⇒ Phương trình có hai nghiệm.
+ Với 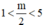 ⇔ 2 < m < 10.
⇔ 2 < m < 10.
⇒ Đường thẳng cắt đồ thị hàm số tại 3 điểm
⇒ Phương trình có ba nghiệm phân biệt.
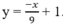


f(x)=-x^2+3x+2=2+9/4-(x^2-2.3/2x+9/4) =17/4 -(x-3/2)^2
f(x)<=17/4
f(x)=17/4 -(x-3/2)^2 luôn có 2 nghiệm x1 và x2 => |f(x)| >=0
f(x)<=17/4 => |f(x)| <=17 /4 khi x thuộc (x1;x2)
=>biên luận
nếu 2m-1 =0 => f(x) =2m-1 có 2 nghiệm x1, x2
nếu 2m-1 <0 => f(x) =2m-1 vô nghiệm
nếu 2m-1 =17/4 => f(x) =2m-1 có 3 nghiệm
nếu 2m-1 >17/4 => f(x) =2m-1 có 2 nghiệm
0<nếu 2m-1 <17/4 => f(x) =2m-1 có 4 nghiệm
Bạn tự giải ra m