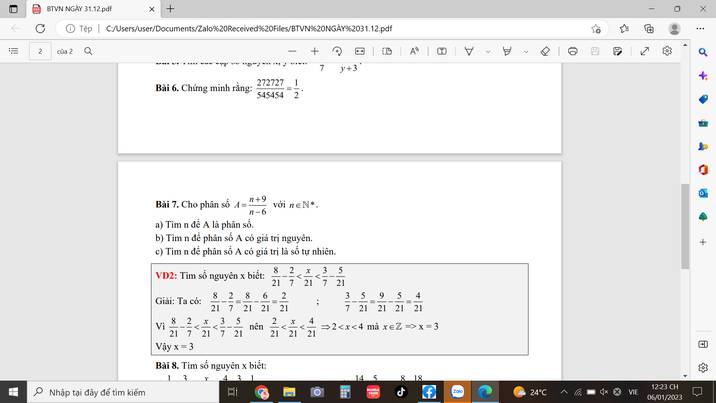
Giải giúp mình bài 
7 và bài 8 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
1
Những câu hỏi liên quan
3L
2
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
LN
giúp mình bài 7, bài 8 với ạ, cảm ơn nhiều
0
NH
1
AH
Akai Haruma
Giáo viên
6 tháng 1 2023
Lời giải:
a. Để $n$ là phân số thì $n-6\neq 0$ hay $n\neq 6$
b. Để $A$ nguyên thì $n+9\vdots n-6$
$\Rightarrow (n-6)+15\vdots n-6$
$\Rightarrow 15\vdots n-6$
$\Rightarrow n-6\in\left\{\pm 1; \pm 3; \pm 5; \pm 15\right\}$
$\Rightarrow n\in\left\{7; 5; 9; 3; 11; 1; -9; 21\right\}$
Do $n$ là số tự nhiên lớn hơn $0$ nên $n\in\left\{7; 5; 9; 3; 11; 1; 21\right\}$
c.
Để $A$ tự nhiên thì $A>0$ và $A$ nguyên
$A>0$ khi mà $n-6>0$ hay $n>6$
$A$ nguyên khi mà $n\in\left\{7; 5; 9; 3; 11; 1; 21\right\}$ (đã cm ở phần b)
Suy ra để $A>0$ và nguyên thì $n\in\left\{7; 9; 11; 21\right\}$
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 3 2023
em ơi chưa có bài em nhé, em chưa tải bài lên lám sao mình giúp được
NH
0
SN
1 tháng 3 2017
Bài 39
Gọi x ( đồng ) là tiền mua loại hàng thứ nhất không kể VAT ( 0 < x < 110 000 )
Tiền mua loại hàng thứ nhất không kể VAT là 110 000 - x
Số tiền thực sự Lan đã trả cho loại hàng 1 : x + 0,1x
Số tiền thực sự Lan đã trả cho loại hàng 2 :
110 000 - x + 0,08 ( 110 000 - x )
Ta có phương trình
\(x+0,1x+110000-x+0,08\left(110000-x=120000\right)\)
=> 0,1x + 110 000 + 8800 - 0,08 x = 120000
=> 0,02 x = 1200
=> x = 6000
Vậy số tiền phải trả cho loại hàng thứ nhất là 6000
Số tiền phải trả cho loại hàng thứ 2 không kể VAT là 5000
Ủng hộ tk Đúng nhé bạn !
1 tháng 3 2017
nhiều bài 39 , 42 lắm đấy , bạn phải nói trang bn chứ
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Bài 7:
a: \(P=\dfrac{x-1}{\sqrt{x}}:\dfrac{x-1+1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-\sqrt{x}}=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}>0\)
b: Thay \(x=\dfrac{2}{2+\sqrt{3}}=4-2\sqrt{3}\) vào P, ta được:
\(P=\dfrac{\left(\sqrt{3}-1+1\right)^2}{\sqrt{3}-1}=\dfrac{3}{\sqrt{3}-1}=\dfrac{3\sqrt{3}+3}{2}\)