Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D và trên tia đối của tia CA lấy điểm E sao cho CE=BD. Gọi I là giao điểm của BC và DE. CMR: DI=IE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
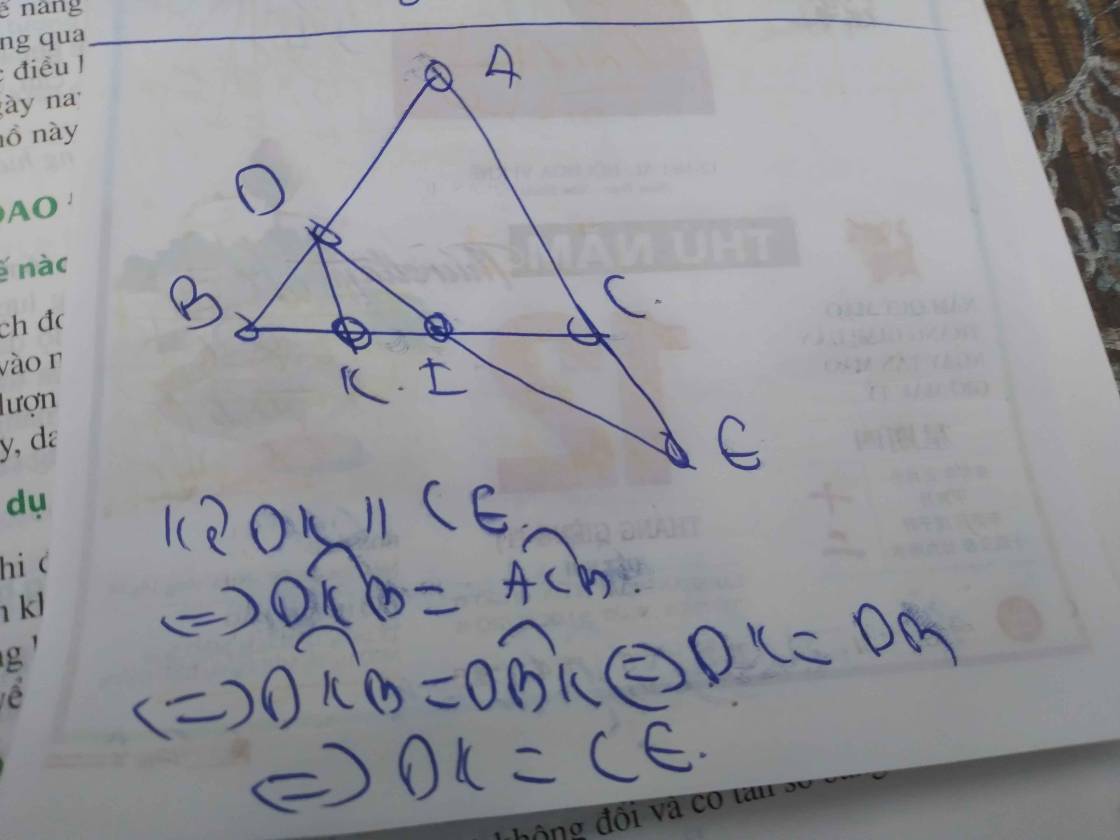

Hình của Tuấn Anh nha!!
Dựng DH// CE
\(\Rightarrow\widehat{HDI}=\widehat{CEI}\left(slt\right);\widehat{DHC}=\widehat{BCE}\left(slt\right)\)
mà \(\widehat{DHC}+\widehat{DHB}=180^o;\widehat{BCE}+\widehat{BCA}=180^o\)
\(\Rightarrow\widehat{DHB}=\widehat{BCA}\)
mặt khác\(\widehat{ABC}=\widehat{ACB}\) (tam giác ABC cân tại A)
\(\Rightarrow\widehat{DHB}=\widehat{DBH}\)
=> tam giác DHB cân tại D => DB=DH
mà DB=CE(gt) nên DH=CE
Ta có:
\(\left\{{}\begin{matrix}\widehat{HDI}=\widehat{CEI}\left(cmt\right)\\DH=CE\left(cmt\right)\\\widehat{DHC}=\widehat{ECB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta DHI=\Delta ECI\) (g.c.g)
=> DI=EI (cặp cạnh tương ứng) (đpcm)
Chúc bạn học tốt!!!