1>Cho biểu thức: Q= \(\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}+\dfrac{2\sqrt{x}}{x-4}\)
a) Rút gọn biểu thức Q
b) tìm x để Q = \(\dfrac{6}{5}\)
c) tìm các giá trị nguyên của x để biểu thức Q có giá trị nguyên
2> Tính:
a) \(\sqrt{16a}+2\sqrt{40a}-3\sqrt{90a}\left(a\ge0\right)\)
b)\(\left(2\sqrt{3}+5\right)\sqrt{3}-\sqrt{60}\)
c)\(\left(\sqrt{99}-\sqrt{8}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
Các bạn giúp mình với .Cảm...
Đọc tiếp
1>Cho biểu thức: Q= \(\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}+\dfrac{2\sqrt{x}}{x-4}\)
a) Rút gọn biểu thức Q
b) tìm x để Q = \(\dfrac{6}{5}\)
c) tìm các giá trị nguyên của x để biểu thức Q có giá trị nguyên
2> Tính:
a) \(\sqrt{16a}+2\sqrt{40a}-3\sqrt{90a}\left(a\ge0\right)\)
b)\(\left(2\sqrt{3}+5\right)\sqrt{3}-\sqrt{60}\)
c)\(\left(\sqrt{99}-\sqrt{8}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
Các bạn giúp mình với 
.Cảm ơn!!
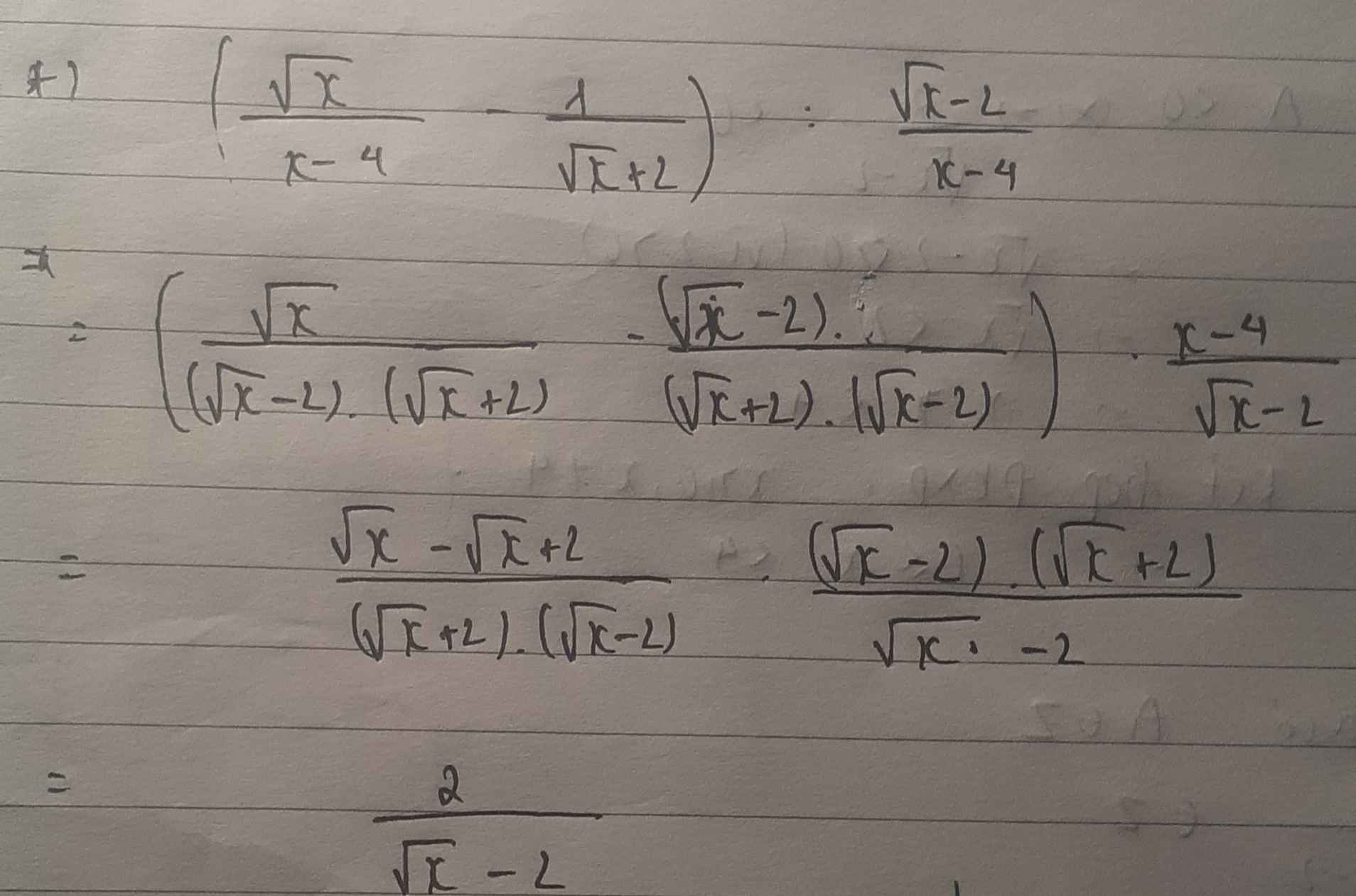
đk : \(x\ne4\) ; \(x\ge0\)
1) a) Q = \(\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}+\dfrac{2\sqrt{x}}{x-4}\)
Q = \(\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}-\dfrac{2\sqrt{x}}{4-x}\)
Q = \(\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}-\dfrac{2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
Q = \(\dfrac{2\left(2-\sqrt{x}\right)+2+\sqrt{x}-2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
Q = \(\dfrac{4-2\sqrt{x}+2+\sqrt{x}-2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
Q = \(\dfrac{6-3\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\) = \(\dfrac{3\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
Q = \(\dfrac{3}{2+\sqrt{x}}\)
b) ta có Q = \(\dfrac{6}{5}\) \(\Leftrightarrow\) \(\dfrac{3}{2+\sqrt{x}}\) = \(\dfrac{6}{5}\) \(\Leftrightarrow\) \(\dfrac{6}{4+2\sqrt{x}}\) = \(\dfrac{6}{5}\)
\(\Leftrightarrow\) \(4+2\sqrt{x}=5\) \(\Leftrightarrow\) \(2\sqrt{x}=1\) \(\Leftrightarrow\) \(\sqrt{x}=\dfrac{1}{2}\) \(\Leftrightarrow\) \(x=\dfrac{1}{4}\)
c) điều x nguyên ; x \(\ge\) 0 ; x\(\ne\) 4
ta có Q nguyên \(\Leftrightarrow\) \(\dfrac{3}{2+\sqrt{x}}\) nguyên
\(\Rightarrow\) \(2+\sqrt{x}\) là ước của 3 là 3 ; 1 ; -1 ; -3
mà \(2+\sqrt{x}\ge2\) (đk :\(x\ge0\)) vậy còn lại 3
\(\Leftrightarrow\) \(2+\sqrt{x}=3\) \(\Leftrightarrow\) x = 1 (tmđk)
vậy x = 1 nguyên thì Q nguyên
2) a) \(\sqrt{16a}+2\sqrt{40a}-3\sqrt{90a}\) = \(4\sqrt{a}+4\sqrt{10a}-9\sqrt{10a}\)
= \(4\sqrt{a}-5\sqrt{10a}\)
b) \(\left(2\sqrt{3}+5\right)\sqrt{3}-\sqrt{60}\) = \(6+5\sqrt{3}-\sqrt{60}\)
c) \(\left(\sqrt{99}-\sqrt{8}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
= \(33-2\sqrt{22}-11+3\sqrt{22}\)
= \(22+\sqrt{22}\)