1) Xác định hệ số a;b để đa thức sau là bình phương của 1 đa thức
A = \(x^4-2x^3-x^2+ax+b\)
2) Tìm số dư trong phép chia
a) \(44^{20}\) cho 15
b) \(3^{123}\) cho 80
Giúp mk giải chi tiết nha!!! Đang cần gấp![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Bậc là 2
Hệ số cao nhất là -7
Hệ số tự do là 1
b: Thay x=2 vào A=0, ta được:
\(a\cdot2^2-3\cdot2-18=0\)
\(\Leftrightarrow4a=24\)
hay a=6
c: Ta có: C+B=A
nên C=A-B
\(=6x^2-3x-18-1-4x+7x^2\)
\(=13x^2-7x-19\)

Đáp án D
Đồ thị hàm số đi qua điểm A(2; 1) thì 1 = a.2 + 1 ⇒ a = 0
Vậy giá trị cần tìm là a = 0

Đáp án B
Do hệ phương trình đã cho có nghiệm là (1; 1) nên:
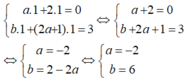
Vậy a = -2; b = 6
2/ Áp dụng phép đồng dư
a) \(44^{20}:15\)
Ta có: \(44^2\equiv1\left(mod15\right)\)
\(\left(44^2\right)^{10}\equiv1^{10}\equiv1\left(mod15\right)\)
=> Số dư trong phép chia \(44^{20}\) cho 15 là 1
b) \(3^{123}:80\)
Ta có: \(3^4\equiv1\left(mod80\right)\)
\(\left(3^4\right)^{30}\equiv1^{30}\equiv1\left(mod80\right)\)
Có: \(3^{120}\cdot3^3\equiv1\cdot27\equiv27\left(mod80\right)\)
Vậy số dư trong phép chia \(3^{123}\) cho 80 là 27
1)
\(P=\left(x^2+mx+1\right)^2\) hoặc \(P=\left(x^2+mx-1\right)\) do hệ số \(x^4\) là 1; hệ số tự do là 1.
+ Với \(P=\left(x^2+mx+1\right)^2=x^4+2mx^3+\left(m^2+2\right)x^2+2mx+1=x^4+ax^3+bx^2-8x+1\)\(\Rightarrow2m=-8;a=2m;b=m^2+2\)
\(\Rightarrow m=-4;a=-8;b=18\)
+ Với\(P=\left(x^2+mx-1\right)^2=x^4+2mx^3+\left(m^2-2\right)x^2-2mx+1\)
Làm tương tự được m = 4; a = 8; b = 14