khi dòng điện có cường độ 2A chạy qua một dây dẫn có điện trở 50\(\Omega\) thì tỏa ra một nhiệt lượng là 180kj hỏi thời gian dòng điện chạy qua vật ẫn đó là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
thì toả ra một nhiệt lượng là 180 kJ. Hỏi thời gian dòng điện chạy qua vật dẫn đó là bao nhiêu?
B. 
VT
29 tháng 7 2018
Đáp án B
Nhiệt lượng tỏa ra Q = I 2 R t = 2 2 . 20 . 30 . 60 = 144 000 J
TP
23 tháng 1 2020
1.Đổi 10 phút=600s
540kJ=540000J
Ta có Q=I2.R.t
\(\Leftrightarrow\)540000=32.R.600
\(\Rightarrow\)R=100\(\Omega\)
TP
23 tháng 1 2020
2.Đổi 180kJ=180000J
Ta có Q=I2.R.t
\(\Leftrightarrow\)180000=22.50.t
\(\Rightarrow\)t=900s (=15 phút)
CM
4 tháng 7 2017
Nhiệt lượng tỏa ra là 60 calo nghĩa là Q = 60.
Ta có : 60 = 2,4 I 2 ⇒ I 2 = 60/(2,4) = 25
Vậy I = 5 (A).
6 tháng 1 2021
Đổi : 10' = 600s
NL tỏa ra ở dây dẫn đó là :
\(Q=U.I.t=I^2.R.t=0,2^2.3000.600=72000J\)
VT
11 tháng 3 2017
Chọn A. Phát biểu không đúng : Nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua tỉ lệ thuận với cường độ dòng điện, với điện trở của dây dẫn và với thời gian dòng điện chạy qua
Nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua tỷ lệ thuận với bình phương cường độ dòng điện, với điện trở của dây dẫn và thời gian dòng điện chạy qua.
Hệ thức: Q = I 2 .R.t (trong đó: I là cường độ dòng điện (A), R là điện trở dây dẫn (Q), t là thời gian dòng điện chạy qua (s), Q là nhiệt ìượng tỏa ra (J)).
Mặt khác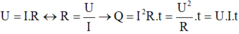
VT
16 tháng 4 2018
Đáp án C
Phương pháp: Công thức tính nhiệt lượng tỏa ra trong thời gian t : Q = I 2 R t
Cách giải:
Nhiệt lượng to ra: Q = I 2 R t = 2 2 .200.40 = 32000 J = 32 k J
Q = 180kj = 180000j
Ta có Q = A = I2Rt
=> t = \(\dfrac{Q}{I^2R}\)= \(\dfrac{180000}{2^2\cdot50}\)=900s = 15 phút = 1/4 giờ
TICK NHA
