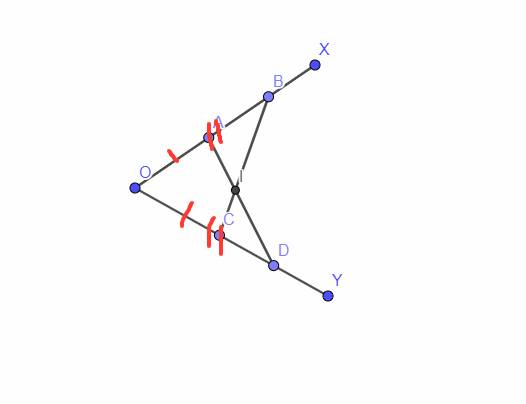
cho góc nhọn xOy. trên tia Ox lấy các đoạn OA=4,OB=8. trên tia OY lấy các đoạn OC=2, OD=4.
a) chứng minh tam giác OAC đồng dạng với tam, giác OBD.
b) gọi I là giao điểm của AD và BC. chứng minh: IA.ID=IB.IC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 3 2023
\(\text{#TuanNam}\)
`a,` Mình xp sửa đề câu a: cm: Tam giác `OAD =` Tam giác `OCB (` vì nếu là `OCD` thì k đúng, vì `3` điểm đó thẳng hàng `)`.
Xét Tam giác `OAD` và Tam giác `OCB` có:
`OA=OC (g``t)`
\(\widehat{O}\) chung
`OB=OD (g``t)`
`=>` Tam giác `OAD =` Tam giác `OCB (c-g-c)`
`b,` Hnhu đề bị sai ;-;
`
HN
2 tháng 12 2021
a: Xét ΔOAD và ΔOCB có
OA=OC
ˆOO^ chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
Y
a: Xét ΔOAC và ΔOBD có
OA/OB=OC/OD
góc AOC chung
Do dó: ΔOAC đồng dạng với ΔOBD
b: Xét ΔIAB và ΔICD có
\(\widehat{IBA}=\widehat{IDC}\)
\(\widehat{AIB}=\widehat{CID}\)
DO đó: ΔIAB\(\sim\)ΔICD
Suy ra: IA/IC=IB/ID
hay \(IA\cdot ID=IB\cdot IC\)