Question

[Nguyễn Mai Phương]

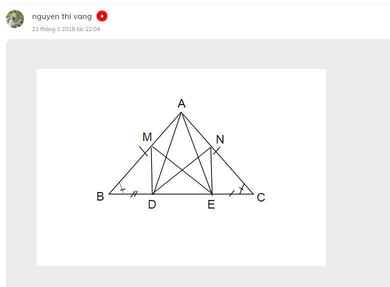
Cho tam giác ABC vuông ở A. Trên cạnh BC lấy điểm D sao cho BD=AB. Qua D kẻ đường thẳng vuông góc với BC, đường thẳng này cắt cạnh AC tại E

a) Tính độ dài cạnh AC nếu cho AB=3cm, BC=5cm

b)Chứng minh BE là đường trung trực của đoạn thẳng AD

c) So sánh độ dài hai đoạn thẳng AE và EC

d) Hạ AK \(\perp\) BC (K\(\in\)BC) . Gọi giao điểm của AK và BE là H. Chứng minh DH song song với AC

e) Chứng minh DK<DC

Giúp mình với !!!!!Mình đang cần gấp !!!! Thanks mn

Answer 1

[Hải Ngân]

a) \(\Delta ABC\) vuông tại A theo định lí Py-ta-go

Ta có: BC² = AB² + AC²

\(\Rightarrow\) AC² = BC² - AB²

AC² = 5² - 3²

AC² = 16

\(\Rightarrow\) AC = \(\sqrt{16}=4\left(cm\right)\)

b) Xét hai tam giác vuông ABE và DBE có:

AB = BD (gt)

BE: cạnh chung

Vậy: \(\Delta ABE=\Delta DBE\left(ch-cgv\right)\)

Suy ra: AE = DE (hai cạnh tương ứng) (1)

Mà AB = BD (gt) (2)

Từ (1) và (2) suy ra:

BE là đường trung trục của đoạn thẳng AD (đpcm)

c) Vì \(\Delta EDC\) vuông tại D

\(\Rightarrow\) DE < EC (đường vuông góc ngắn hơn đường xiên)

Mà AE = DE (cmt)

Do đó: AE < EC

e) Vì \(\Delta AKC\) vuông tại K

\(\Rightarrow\) AK < AC (đường vuông góc ngắn hơn đường xiên)

\(\Rightarrow\) DK < DC (quan hệ giữa đường xiên và hình chiếu của chúng).

Answer 2

[Phạm Ánh Tuyết]

Gọi giao điểm của AB và DH là M và giao điểm của BE và AD là I

Vì BE là đường trung trực của AD hay BI là đường trung trực của AD

=>IA=ID và BI\(\perp\)AD

Xét 2\(\Delta\)vuông: \(\Delta\)AIH và \(\Delta\)DIH,có:

HI:cạnh chung

IA=ID(cmt)

=>\(\Delta\)AIH=\(\Delta\)DIH(c.g.c)

=>^AHI=^DHI(2 góc tương ứng)(1)

Lại có:

^AHI=^BHK(2 góc đối đỉnh)(2)

^DHI=^BHM(3)

Từ (1),(2) và (3)

=>^BHK=^BHM

Vì \(\Delta\)BAD cân tại B(do AB=DB)

Mà BI là đường trung trực của \(\Delta\)BAD

=>BI đồng thời là đường phân giác của \(\Delta\)BAD

=>^ABI=^DBI hay ^MBH=^KBH

Xét \(\Delta\)BHM và \(\Delta\)BHK , có:

^MBH=^KBH(cmt)

BH:cạnh chung

^BHM=^BHK(cmt)

=>\(\Delta\)BHM=\(\Delta\)BHK(g.c.g)

=>^BMH=^BKH(2 góc tương ứng)

=>^BMH=90⁰

=>HD\(\perp\)AB

Mà AC \(\perp\)AB( do \(\Delta\)ABC vuông tại A)

=>HD//AC

Vậy HD//AC