cho tam giác DEF vuông tại D có DE=12cm, DF=20cm. kẻ đường cao DH (H ∈ EF)
a) chứng minh: DF.ED=FE.DH
b) tính DF, EH, HF
c) kẻ HN⊥DE tại N (N∈DE), HM⊥DF tại M (M∈DF) chứng minh: ∇DMN∾∇DEF
d) chứng minh: DN/DE+DM/DF=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(S_{DEF}=\dfrac{DE\cdot DF}{2}=\dfrac{DH\cdot FE}{2}\)
nên \(DE\cdot DF=DH\cdot FE\)
c: Xét ΔDHE vuông tại H có HN là đường cao
nên \(DN\cdot DE=DH^2\left(1\right)\)
XétΔDHF vuông tại H có HM là đường cao
nên \(DM\cdot DF=DH^2\left(2\right)\)
Từ(1) và (2) suy ra \(DN\cdot DE=DM\cdot DF\)
hay DN/DF=DM/DE
Xét ΔDNM vuông tại D và ΔDFE vuông tại D có
DN/DF=DM/DE
Do đó: ΔDNM\(\sim\)ΔDFE

\(\text{#TNam}\)
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`
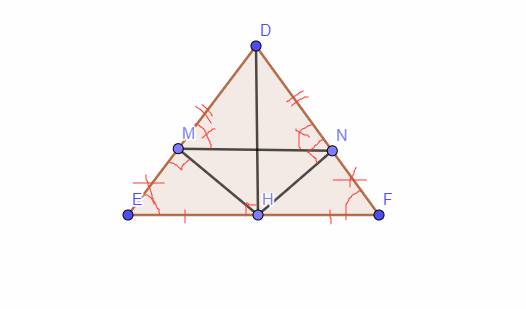

a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó:ΔDHE=ΔDHF
b: EF=8cm nên HE=4cm
=>DH=3cm
c: Xét ΔDMH vuông tại M và ΔDNH vuông tại N có
DH chung
\(\widehat{MDH}=\widehat{NDH}\)
Do đó:ΔDMH=ΔDNH
Suy ra: HM=HN
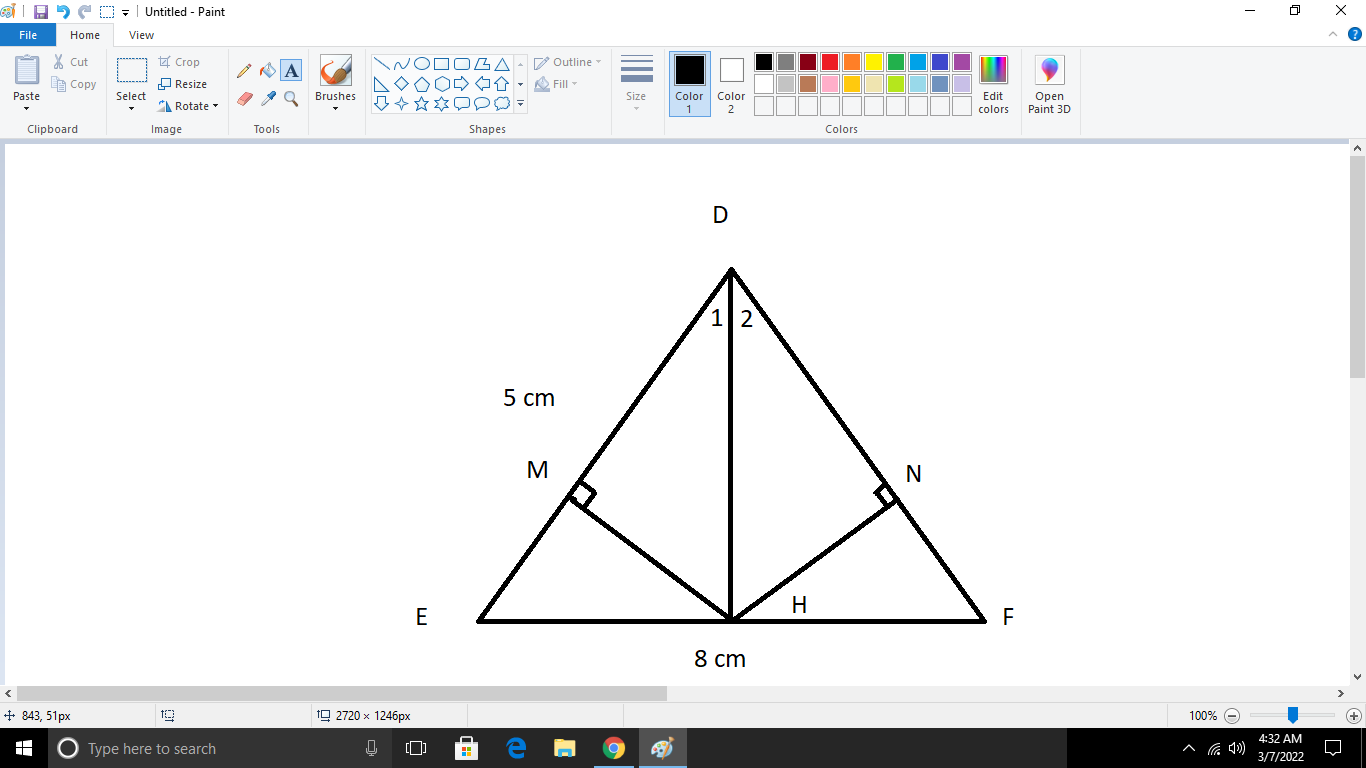
\(\text{a)}\text{Vì }\Delta DEF\text{ cân tại D}\)
\(\Rightarrow DE=DF\)
\(\widehat{E}=\widehat{F}\)
\(\text{Xét }\Delta DHE\text{ và }\Delta AHF\text{ có:}\)
\(DE=DF\left(cmt\right)\)
\(BH\text{ chung}\)
\(\widehat{E}=\widehat{F}\left(cmt\right)\)
\(\Rightarrow\Delta DHE=\Delta DHF\left(c-g-c\right)\)
\(\Rightarrow EH=HF\text{(hai cạnh tương ứng)}\)
\(\text{b)}\text{Vì }EH=HF\left(cmt\right)\)
\(\Rightarrow EH=\dfrac{EF}{2}=\dfrac{8}{2}=4\left(cm\right)\)
\(\text{Xét }\Delta DEH\text{ có:}\)
\(DE^2=DH^2+EH^2\)
\(\Rightarrow DH^2=DE^2-EH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow DH^2=5^2-4^2=25-16=9\left(cm\right)\)
\(\Rightarrow DH=\sqrt{9cm}=3\left(cm\right)\)
\(\text{c)Xét }\Delta HMD\text{ và }\Delta HND\text{ có:}\)
\(DH\text{ chung}\)
\(\widehat{D_1}=\widehat{D_2}\left(\Delta DHE=\Delta DHF\right)\)
\(\widehat{DMH}=\widehat{DNH}=90^0\)
\(\Rightarrow\Delta HMD=\Delta HND\left(ch-cgv\right)\)
\(\Rightarrow HM=HN\text{( hai cạnh tương ứng)}\)

a: \(DE=\sqrt{15^2-12^2}=9\left(cm\right)\)
\(S_{DEF}=\dfrac{1}{2}\cdot9\cdot12=6\cdot9=54\left(cm^2\right)\)
b: Xét tứ giác DMHN có
góc DMH=góc DNH=góc MDN=90 độ
nên DMHN là hình chữ nhật
c: Xét tứ giác DHMK có
DK//MH
DK=MH
Do đó: DHMK là hình bình hành