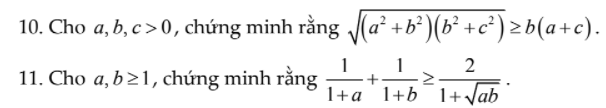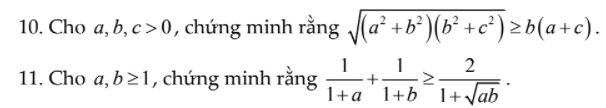Ai giải hộ mình câu 44 với cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
!
HP
1 tháng 9 2021
10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
HP
1 tháng 9 2021
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)
A
1
A
0
N
12
AM
1
1 tháng 11 2021
Câu 1:
TXĐ:D=R
\(f\left(-x\right)=2\cdot\left(-x\right)^4-3\cdot\left(-x\right)^2+1\)
\(=2x^4-3x^2+1=f\left(x\right)\)
=>f(x) là hàm số chẵn
H
12 tháng 5 2021
a) mNaCl = 2,5.0,9% = 0,0225(kg)
m H2O = 2,5 -0,0225 = 2,4775 (kg)
- Cân lấy 0,0225 kg NaCl cho vào cốc
- Đong lấy 2,4775 kg nước cho vào cốc, khuấy đều
b)
m MgCl2 =50.4% = 2(gam)
m H2O = 50 - 2 = 48(gam)
- Cân lấy 2 gam MgCl2 cho vào cốc
- Đong lấy 48 gam nước cho vào cốc, khuấy đều
c)
m MgSO4 = 250.0,1% = 0,25(gam)
m H2O = 250 - 0,25 = 249,75 gam
- Cân lấy 0,25 gam MgSO4 cho vào cốc
- Đong lấy 249,75 gam MgSO4 cho vào cốc, khuấy đều
d)
n NACl = 0,5.0,5 = 0,25(mol)
m NaCl = 0,25.58,5 = 14,625 gam
- Cân lấy 14,625 gam NaCl cho vào cốc có chia vạch
- Thêm từ từ nước vào cho đến khi chạm vạch 500 ml thì dừng lại,khuấy đều
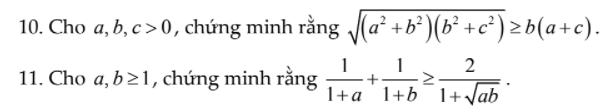