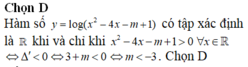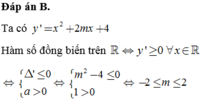Tìm tất cả các giá trị của m để hàm số y = √x2+4x−8+mx2+4x−8+m xác định trên [ 0;8 ]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hàm xác định trên \(\left[0;8\right]\) khi và chỉ khi với mọi \(x\in\left[0;8\right]\) ta có:
\(x^2+4x-8+m\ge0\)
\(\Leftrightarrow m\ge-x^2-4x+8\)
\(\Leftrightarrow m\ge\max\limits_{\left[0;8\right]}\left(-x^2-4x+8\right)\)
Xét hàm \(f\left(x\right)=-x^2-4x+8\) trên \(\left[0;8\right]\)
\(-\dfrac{b}{2a}=-2< 0\Rightarrow\) hàm nghịch biến trên \(\left[0;8\right]\)
\(\Rightarrow\max\limits_{\left[0;8\right]}f\left(x\right)=f\left(0\right)=8\)
\(\Rightarrow m\ge8\)

Chọn D
Hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ khi và chỉ khi
![]()
![]()

Đáp án B.
Ta có y ' = x 2 + 2 m x + 4
Hàm số đồng biến trên ℝ ⇔ y ' ≥ 0 ∀ x ∈ ℝ .
⇔ ∆ ' ≤ 0 a > 0 ⇔ m 2 - 4 ≤ 0 1 > 0 ⇔ - 2 ≤ m ≤ 2

Đáp án A
y = m 3 x 3 − m x 2 + ( 2 m − 1 ) x − 2 txd D = R
y ' = m x 2 − 2 m x + 2 m − 1
Để hàm số nghịch biến trên R ⇔ y ' ≤ 0 ∀ x ∈ R
⇔ m = 0 m < 0 Δ ' = m 2 − 2 m 2 + m ≤ 0 ⇔ m = 0 m < 0 m ∈ ( − ∞ ; 0 ] ∪ [ 1 ; + ∞ ) ⇔ m ≤ 0

Đáp án C
Ta có y ' = 4 − m 2 x − 1 2 hàm số đồng biến trên tập xác định của nó
⇔ 4 − m 2 > 0 ⇔ − 2 < m < 2 do m nguyên ⇒ m = 0, m = ± 1

Đáp án D
Ta có f x = m x 2 − 4 m + m 2 → f ' x = 2 m x − 4 , ∀ x ∈ ℝ
Bất phương trình f ' x < 0 ; ∀ x ∈ − 1 ; 2 ⇔ m x − 2 < 0 ; ∀ x ∈ − 1 ; 2 ⇔ − 2 ≤ m ≤ 1