a) Vẽ hình và tính số đường chéo của ngũ giác, lục giác
b) Chứng minh rằng hình - n giác có tất cả \(\dfrac{n\left(n-3\right)}{2}\) đường chéo
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ mỗi đỉnh của ngũ giác vẽ được 2 đường chéo. Ngũ giác có 5 đỉnh ta kẻ được 5.2=10 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.
Từ mỗi đỉnh của lục giác vẽ được 3 đường chéo. Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả 9 đường chéo.
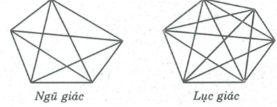

- Từ mỗi đỉnh của ngũ giác vẽ được 2 đường chéo. Khi đó, vẽ được tất cả 2.5 = 10 đường chéo.
Vì mỗi đường chéo được tính hai lần nên ngũ giác có tất cả 5 đường chéo.
- Tương tự: lục giác từ 6 đỉnh vẽ được 3.6 = 18 đường chéo. Vì mỗi đường chéo được tính 2 lần nên lục giác có tất car9 đường chéo.
- Từ mỗi đỉnh của hình n - giác (lồi) vẽ được (n - 1) đoạn thẳng nối đỉnh đó với (n - 1) đỉnh còn lại của đa giác, trong đó hai đoạn thẳng trùng với hai cạnh của đa giác sẽ không tính vào số đường chéo.
Þ Qua mỗi đỉnh của hình n - giác vẽ được n - 1 - 2 = n - 3 đường chéo.
Þ Hình n - giác vẽ được n (n - 3) đường chéo
Vì mỗi đường chéo được tính 2 lần nên hình n - giác có tất cả n ( n − 3 ) 2 đường chéo.

Ta chứng minh khẳng định đúng với mọi n ε N* , n ≥ 4.
Với n = 4, ta có tứ giác nên nó có hai đường chéo.
Mặt khác thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là: 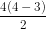 = 2
= 2
Vậy khẳng định là đúng với n= 4.
Giả sử khẳng định là đúng với n = k ≥ 4, tức là đa giác lồi k cạnh có
số đường chéo là 
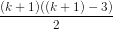 Xét đa giác lồi k + 1 cạnh
Nối A1 và Ak, ta được đa giác k cạnh A1A2…Ak có
Xét đa giác lồi k + 1 cạnh
Nối A1 và Ak, ta được đa giác k cạnh A1A2…Ak có  đường chéo (giả thiết quy nạp). Nối Ak+1 với các đỉnh A2, A3, …, Ak-1, ta được thêm k -2 đường chéo, ngoài ra A1Ak cũng là một đường chéo.
đường chéo (giả thiết quy nạp). Nối Ak+1 với các đỉnh A2, A3, …, Ak-1, ta được thêm k -2 đường chéo, ngoài ra A1Ak cũng là một đường chéo.
Vậy số đường chéo của đa giác k + 1 cạnh là
 + k - 2 + 1 =
+ k - 2 + 1 = 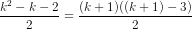
Như vậy, khẳng định cũng đúng với đa giác k + 1 cạnh

Từ mỗi đỉnh của n-giác nối với các đỉnh còn lại ta được n – 1 đoạn thẳng, trong đó có 2 đoạn thẳng là cạnh của hình n-giác (hai đoạn thẳng nối với hai đỉnh kề nhau).
Vậy qua mỗi đỉnh n-giác vẽ được n-3 đường chéo. Hình n-giác có n đỉnh kẻ được n(n- 3) đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy hình n-giác có tất cả n n - 3 2 đường chéo.

THAM KHẢO
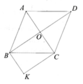
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông