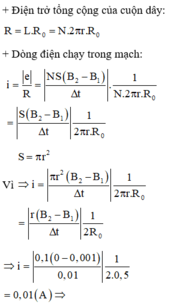một cuộn dây dẹt hình tròn gồm N=100 vòng dây , mỗi vòng có bán kính R=10cm , mỗi mét dài của dây có điện trở Ro=10\(\Omega\) . cuộn dây đặt trong từ trường đều , vectơ cảm ứng từ vuông góc mặt phẳng khung dây và có độ lớn B=10-2T giảm đều đến 0 trong thời gian t=10-2T . tính cường độ dòng điện xuất hiện trong mạch .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong khoảng thời gian ∆ t, từ thông qua cuộn dây dẫn biến thiên một lượng :
![]()
Áp dụng công thức của định luật Fa – ra – đây: ta xác định được độ lớn của suất điện động cảm ứng xuất hiện trong cuộn dây dẫn
![]()
Các vòng của cuộn dây dẫn có độ dài tổng cộng l = N π d . Vì mỗi mét dài của dây dẫn có điện trở R 0 = 0,5 Ω , nên điện trở của cả cuộn dây dẫn tính bằng : R = I R 0 = N π d R 0 . Từ đó suy ra cường độ dòng điện cảm ứng chạy trong cuộn dây dẫn :
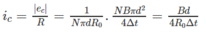
Thay số, ta tìm được : i c = 10mA
![]()

Diện tích mỗi vòng dây:
S = π . ( d 2 ) 2 = 3 , 14. ( 20.10 − 2 2 ) 2 = 0,0314 = 314 . 10 - 4 ( m 2 )
Điện trở của ống dây: R = 1000 . π . d . 0 , 5 = 314 ( Ω ) .
Góc giữa B → và pháp tuyến α là α = n → , B → = 0 °
ϕ = N . B . S . cos n → , B → = 1000 . B . 314 . 10 - 4 . 1 = 31 , 4 . B
e C = Δ Φ Δ t = | Φ 2 − Φ 1 | Δ t = | 31 , 4.0 − 31 , 4.10 − 3 | 10 − 2 = 3 , 14 ( V ) .
I = | e C | R = 3 , 14 314 = 0 , 01 ( A ) .

1 . Độ lớn suất điện động cảm ứng xuất hiện ở 2 đầu cuộn dây :
\(\left|e_c\right|=N.S\dfrac{\left|\Delta B\right|}{\Delta t}.cos\alpha=20.0,1^2.\dfrac{0,2}{10^{-2}}.1=4\) (V)
2 . Cường độ dòng điện xuất hiện trong cuộn dây :
i \(=\dfrac{\left|e_c\right|}{R}=\dfrac{4}{5}=0,8\left(A\right)\)