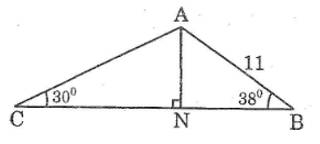
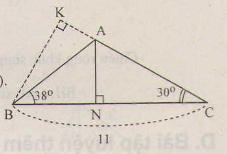
Trong tam giác ABC có \(AB=11cm,\widehat{ABC}=38^0;\widehat{ACB}=30^0\), N là chân đường vuông góc kẻ từ A đến BC (h.18).
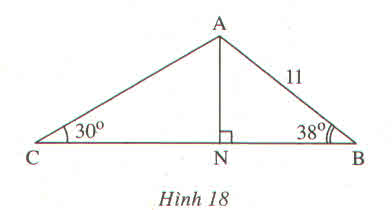
Hãy tính AN, AC ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)

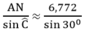
Xét ΔANB vuông tại N có
\(AN=AB\cdot\sin B\)
nên \(AN\simeq6,772\left(cm\right)\)
XétΔACN vuông tại N có
\(AC=\dfrac{AN}{\sin C}=13,544\left(cm\right)\)