Cho hình 13 :
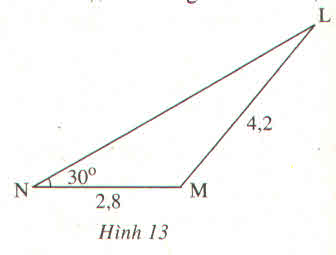
Hãy tính sin L (làm tròn đến chữ số thập phân thứ tư), biết rằng \(\sin30^0=0,5\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2019
a)
xét tam giác ABH vuông tại H có:
\(AH^2=AB^2-BH^2\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{13^2-5^2}=12\)
theo tỉ lệ thức trong tam giác vuông ABC có:
\(AH^2=BH.CH\Rightarrow HC=\frac{AH^2}{BH}=\frac{12^2}{5}=\frac{144}{5}=28,8\)
xét tam giác vuông AHC có:
\(AC^2=AH^2+HC^2\Rightarrow AC=\sqrt{AH^2+HC^2}=\sqrt{12^2+28,8^2}=\frac{156}{5}=31,2\)
vậy : \(\sin B=\frac{AH}{AB}=\frac{12}{13}\)
\(\sin C=\frac{AH}{AC}=\frac{12}{31,2}=\frac{5}{13}\)
b)
theo tỉ số lượng giác trong tam giác ABC có:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3.4}=2\sqrt{3}\)
xét tam giác vuông ABH có:
\(AB^2=AH^2+BH^2\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{3}\right)^2+3^2}=\sqrt{21}\)
theo hệ thức lượng trong tam giác vuông ABC có:
\(AC^2=BC.HC\Rightarrow AC=\sqrt{BC.HC}=\sqrt{7.4}=2\sqrt{7}\)
Vậy : \(\sin B=\frac{AH}{AB}=\frac{2\sqrt{3}}{\sqrt{21}}=\frac{2\sqrt{7}}{7}\)
\(\sin C=\frac{AH}{AC}=\frac{2\sqrt{3}}{2\sqrt{7}}=\frac{\sqrt{21}}{7}\)
PT
1
CM
19 tháng 7 2019
Ta có: sin 2 α + c o s 2 α = 1
Suy ra: sin 2 α = 1 - c o s 2 α = 1 - 0 , 8 2 = 1 – 0,64 = 0,36
Vì sin α > 0 nên sin α = 0 , 36 = 0,6
Suy ra: tg α = sin α /cos α = 0,6/0,8 = 3/4 = 0,75
cotg α = 1/tg α = 1/0,75 = 1,3333
PT
1
CM
4 tháng 8 2019
Vì tg α = 1/3 nên α là góc nhọn của một tam giác vuông có các cạnh góc vuông là 1 và 3.
Suy ra cạnh huyền của tam giác vuông là: 
= 3,1623
Vậy: sin α = 3/5 ≈ 0,6 cos α = 4/5 ≈ 0,8
31 tháng 8 2021
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=13^2-5^2=144\)
hay AH=12(cm)
Xét ΔABH vuông tại H có
\(\sin\widehat{B}=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(\Leftrightarrow\cos\widehat{C}=\dfrac{12}{13}\)
hay \(\sin\widehat{C}=\dfrac{5}{13}\)
CM
19 tháng 8 2017
Dùng bảng lượng giác: sin 40o12' ≈ 0,6455
- Cách nhấn máy tính:
